Question Number 100150 by student work last updated on 25/Jun/20
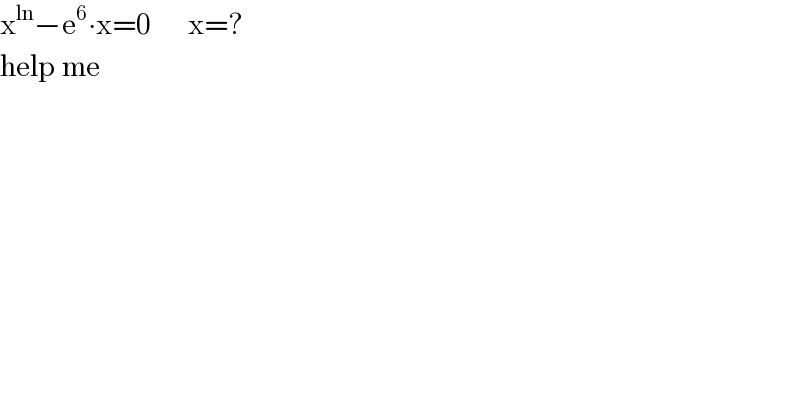
$$\mathrm{x}^{\mathrm{ln}} −\mathrm{e}^{\mathrm{6}} \centerdot\mathrm{x}=\mathrm{0}\:\:\:\:\:\:\mathrm{x}=? \\ $$$$\mathrm{help}\:\mathrm{me} \\ $$
Commented by student work last updated on 25/Jun/20

$$\mathrm{x}^{\mathrm{lnx}} −\mathrm{e}^{\mathrm{6}} \centerdot\mathrm{x}=\mathrm{0} \\ $$
Commented by bobhans last updated on 25/Jun/20

$$\mathrm{your}\:\mathrm{question}\:\mathrm{not}\:\mathrm{clear} \\ $$
Commented by bemath last updated on 25/Jun/20
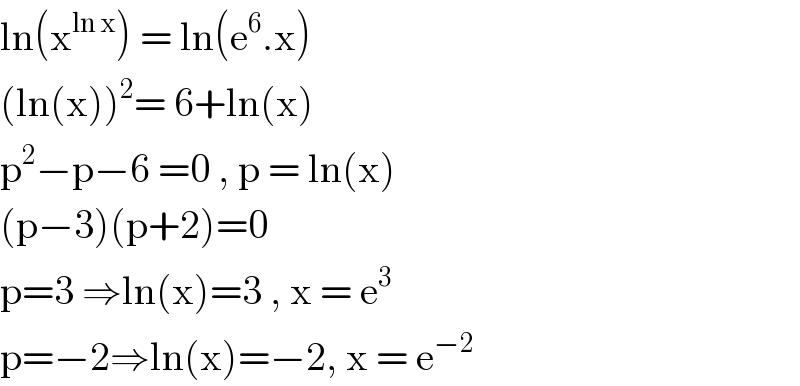
$$\mathrm{ln}\left(\mathrm{x}^{\mathrm{ln}\:\mathrm{x}} \right)\:=\:\mathrm{ln}\left(\mathrm{e}^{\mathrm{6}} .\mathrm{x}\right) \\ $$$$\left(\mathrm{ln}\left(\mathrm{x}\right)\right)^{\mathrm{2}} =\:\mathrm{6}+\mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\mathrm{p}^{\mathrm{2}} −\mathrm{p}−\mathrm{6}\:=\mathrm{0}\:,\:\mathrm{p}\:=\:\mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\left(\mathrm{p}−\mathrm{3}\right)\left(\mathrm{p}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{p}=\mathrm{3}\:\Rightarrow\mathrm{ln}\left(\mathrm{x}\right)=\mathrm{3}\:,\:\mathrm{x}\:=\:\mathrm{e}^{\mathrm{3}} \\ $$$$\mathrm{p}=−\mathrm{2}\Rightarrow\mathrm{ln}\left(\mathrm{x}\right)=−\mathrm{2},\:\mathrm{x}\:=\:\mathrm{e}^{−\mathrm{2}} \\ $$
