x-lnx-2-dx-

Question Number 14243 by tawa tawa last updated on 30/May/17

$$\int\:\left[\mathrm{x}\:\left(\mathrm{lnx}\right)^{\mathrm{2}} \right]\:\mathrm{dx} \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17

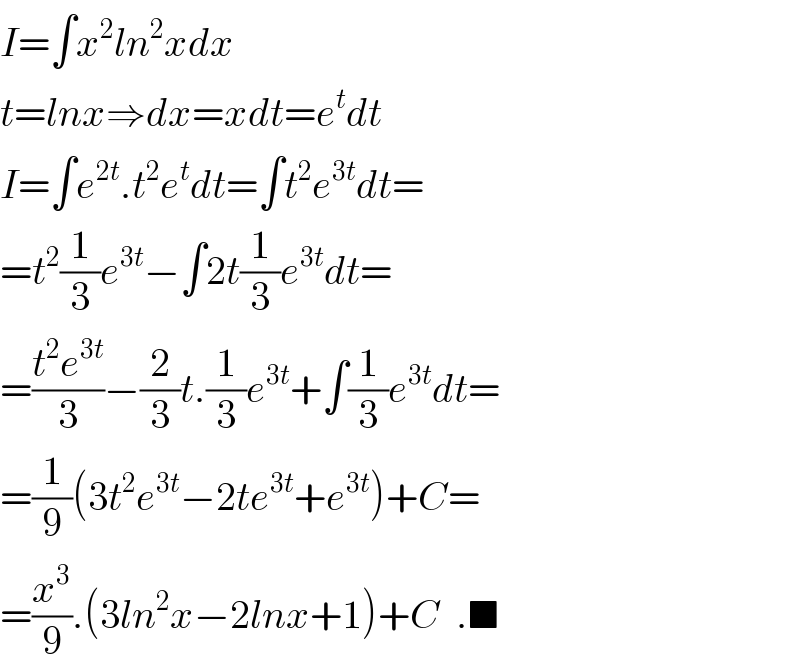
I=∫x^2 ln^2 xdx t=lnx⇒dx=xdt=e^t dt I=∫e^(2t) .t^2 e^t dt=∫t^2 e^(3t) dt= =t^2 (1/3)e^(3t) −∫2t(1/3)e^(3t) dt= =((t^2 e^(3t) )/3)−(2/3)t.(1/3)e^(3t) +∫(1/3)e^(3t) dt= =(1/9)(3t^2 e^(3t) −2te^(3t) +e^(3t) )+C= =(x^3 /9).(3ln^2 x−2lnx+1)+C .■

$${I}=\int{x}^{\mathrm{2}} {ln}^{\mathrm{2}} {xdx} \\ $$$${t}={lnx}\Rightarrow{dx}={xdt}={e}^{{t}} {dt} \\ $$$${I}=\int{e}^{\mathrm{2}{t}} .{t}^{\mathrm{2}} {e}^{{t}} {dt}=\int{t}^{\mathrm{2}} {e}^{\mathrm{3}{t}} {dt}= \\ $$$$={t}^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{t}} −\int\mathrm{2}{t}\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{t}} {dt}= \\ $$$$=\frac{{t}^{\mathrm{2}} {e}^{\mathrm{3}{t}} }{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}{t}.\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{t}} +\int\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{t}} {dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{3}{t}^{\mathrm{2}} {e}^{\mathrm{3}{t}} −\mathrm{2}{te}^{\mathrm{3}{t}} +{e}^{\mathrm{3}{t}} \right)+{C}= \\ $$$$=\frac{{x}^{\mathrm{3}} }{\mathrm{9}}.\left(\mathrm{3}{ln}^{\mathrm{2}} {x}−\mathrm{2}{lnx}+\mathrm{1}\right)+{C}\:\:.\blacksquare \\ $$

Commented by tawa tawa last updated on 30/May/17

sir, i think the square is affecting only lnx as in [x (lnx)^2 ] dx

$$\mathrm{sir},\:\mathrm{i}\:\mathrm{think}\:\mathrm{the}\:\mathrm{square}\:\mathrm{is}\:\mathrm{affecting}\:\mathrm{only}\:\:\mathrm{lnx} \\ $$$$\mathrm{as}\:\mathrm{in}\:\:\:\left[\mathrm{x}\:\left(\mathrm{lnx}\right)^{\mathrm{2}} \right]\:\mathrm{dx} \\ $$

Commented by tawa tawa last updated on 30/May/17

$$\mathrm{Not}\:\:\:\:\left[\mathrm{x}\:\mathrm{ln}\left(\mathrm{x}\right)\right]^{\mathrm{2}} \:\:\:\:\:\mathrm{it}\:\mathrm{is}\:\:\:\left[\mathrm{x}\:\left(\mathrm{lnx}\right)^{\mathrm{2}} \right]\:\mathrm{dx} \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17

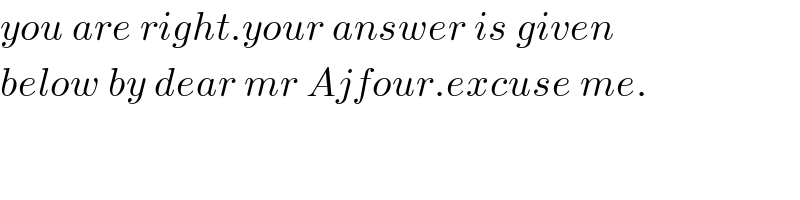
$${you}\:{are}\:{right}.{your}\:{answer}\:{is}\:{given} \\ $$$${below}\:{by}\:{dear}\:{mr}\:{Ajfour}.{excuse}\:{me}. \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17

$${additionaly}\:{now}\:{you}\:{have}\:{answer}\:{of} \\ $$$${another}\:{similar}\:{integral}\:.\blacktriangleright\blacktriangleleft \\ $$

Commented by chux last updated on 30/May/17

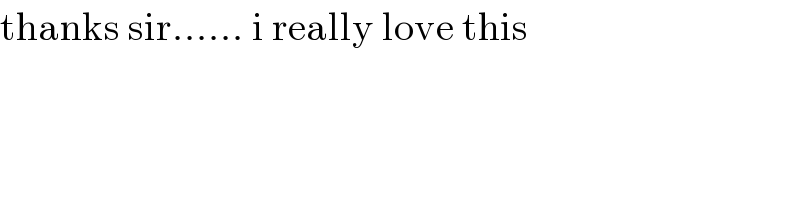
$$\mathrm{thanks}\:\mathrm{sir}……\:\mathrm{i}\:\mathrm{really}\:\mathrm{love}\:\mathrm{this} \\ $$

Commented by tawa tawa last updated on 30/May/17

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by ajfour last updated on 30/May/17

let ln x=t ⇒ x=e^t and dx=e^t dt I=∫[x(ln x)^2 ]dx = ∫e^t (t^2 )(e^t dt)=∫t^2 e^(2t) dt = (t^2 /2)e^(2t) −∫((e^(2t) /2)(2t)dt+C_1 =(t^2 /2)e^(2t) −∫te^(2t) dt+C_1 =(t^2 /2)e^(2t) −[((te^(2t) )/2)−∫ (e^(2t) /2)dt]+C_1 I=(t^2 /2)e^(2t) −((te^(2t) )/2)+(e^(2t) /4)+C_1 +C_2 I=(e^(2t) /4)(2t^2 −2t+1)+C I=(x^2 /4)[2(ln x)^2 −2(ln x)+1]+C .

$${let}\:\mathrm{ln}\:{x}={t}\:\:\:\Rightarrow\:{x}={e}^{{t}} \\ $$$${and}\:\:\:{dx}={e}^{{t}} {dt} \\ $$$$\:{I}=\int\left[{x}\left(\mathrm{ln}\:{x}\right)^{\mathrm{2}} \right]{dx} \\ $$$$\:\:\:=\:\int{e}^{{t}} \left({t}^{\mathrm{2}} \right)\left({e}^{{t}} {dt}\right)=\int{t}^{\mathrm{2}} {e}^{\mathrm{2}{t}} {dt} \\ $$$$\:\:\:=\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}{e}^{\mathrm{2}{t}} −\int\left(\frac{{e}^{\mathrm{2}{t}} }{\mathrm{2}}\left(\mathrm{2}{t}\right){dt}+{C}_{\mathrm{1}} \right. \\ $$$$\:\:\:=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}{e}^{\mathrm{2}{t}} −\int{te}^{\mathrm{2}{t}} {dt}+{C}_{\mathrm{1}} \\ $$$$\:\:\:=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}{e}^{\mathrm{2}{t}} −\left[\frac{{te}^{\mathrm{2}{t}} }{\mathrm{2}}−\int\:\frac{{e}^{\mathrm{2}{t}} }{\mathrm{2}}{dt}\right]+{C}_{\mathrm{1}} \\ $$$$\:{I}=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}{e}^{\mathrm{2}{t}} −\frac{{te}^{\mathrm{2}{t}} }{\mathrm{2}}+\frac{{e}^{\mathrm{2}{t}} }{\mathrm{4}}+{C}_{\mathrm{1}} +{C}_{\mathrm{2}} \\ $$$$\:{I}=\frac{{e}^{\mathrm{2}{t}} }{\mathrm{4}}\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)+\boldsymbol{{C}} \\ $$$$\:{I}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\left[\mathrm{2}\left(\mathrm{ln}\:{x}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{ln}\:{x}\right)+\mathrm{1}\right]+\boldsymbol{{C}}\:. \\ $$

Commented by tawa tawa last updated on 30/May/17

I really apprecate sir. God bless you sir.

$$\mathrm{I}\:\mathrm{really}\:\mathrm{apprecate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply