Question Number 180260 by Mastermind last updated on 09/Nov/22
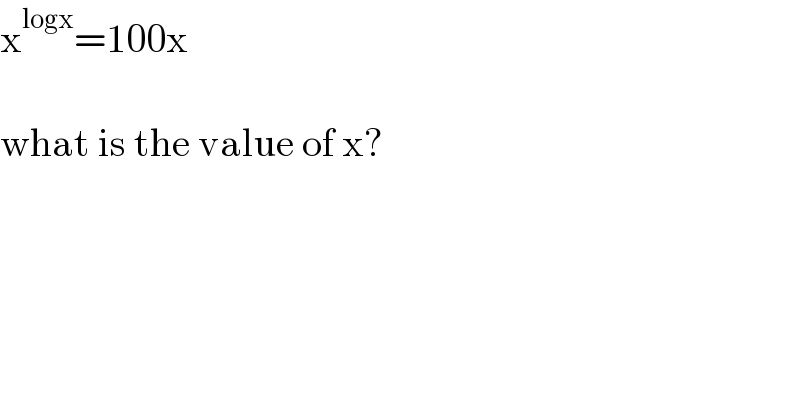
$$\mathrm{x}^{\mathrm{logx}} =\mathrm{100x} \\ $$$$ \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}? \\ $$
Answered by Frix last updated on 09/Nov/22
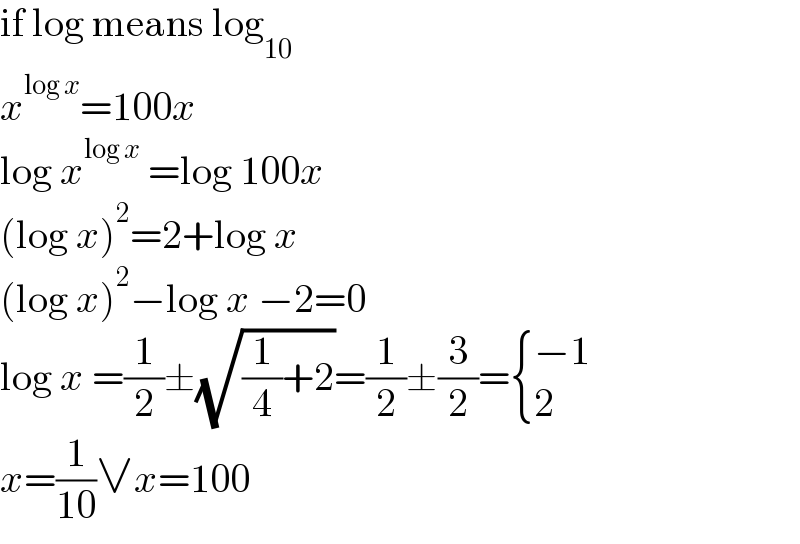
$$\mathrm{if}\:\mathrm{log}\:\mathrm{means}\:\mathrm{log}_{\mathrm{10}} \\ $$$${x}^{\mathrm{log}\:{x}} =\mathrm{100}{x} \\ $$$$\mathrm{log}\:{x}^{\mathrm{log}\:{x}} \:=\mathrm{log}\:\mathrm{100}{x} \\ $$$$\left(\mathrm{log}\:{x}\right)^{\mathrm{2}} =\mathrm{2}+\mathrm{log}\:{x} \\ $$$$\left(\mathrm{log}\:{x}\right)^{\mathrm{2}} −\mathrm{log}\:{x}\:−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{log}\:{x}\:=\frac{\mathrm{1}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\mathrm{3}}{\mathrm{2}}=\begin{cases}{−\mathrm{1}}\\{\mathrm{2}}\end{cases} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{10}}\vee{x}=\mathrm{100} \\ $$
