Question Number 101286 by student work last updated on 01/Jul/20
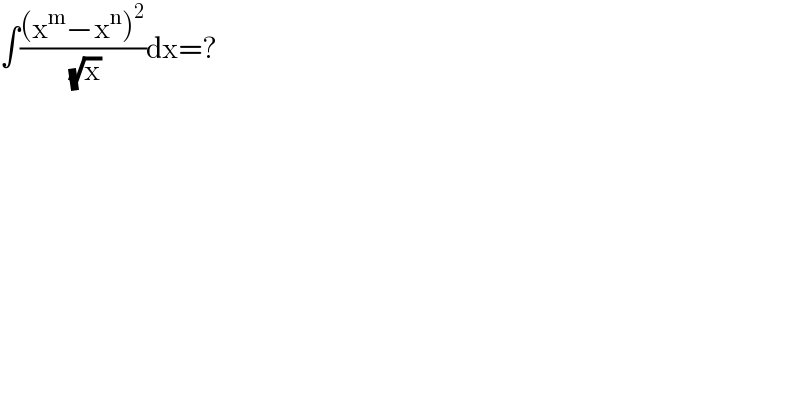
$$\int\frac{\left(\mathrm{x}^{\mathrm{m}} −\mathrm{x}^{\mathrm{n}} \right)^{\mathrm{2}} }{\:\sqrt{\mathrm{x}}}\mathrm{dx}=? \\ $$
Commented by student work last updated on 01/Jul/20

$$\mathrm{I}\:\mathrm{need}\:\mathrm{u}\:\mathrm{help} \\ $$
Commented by prakash jain last updated on 01/Jul/20

$$\mathrm{Expand}\:\left({x}^{{m}} −{x}^{{n}} \right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}{m}} −\mathrm{2}{x}^{{m}} {x}^{{n}} +{x}^{\mathrm{2}{n}} \\ $$$$\mathrm{Divide}\:\mathrm{by}\:\sqrt{{x}}\:\mathrm{and}\:\mathrm{integrate} \\ $$
Commented by Dwaipayan Shikari last updated on 02/Jul/20
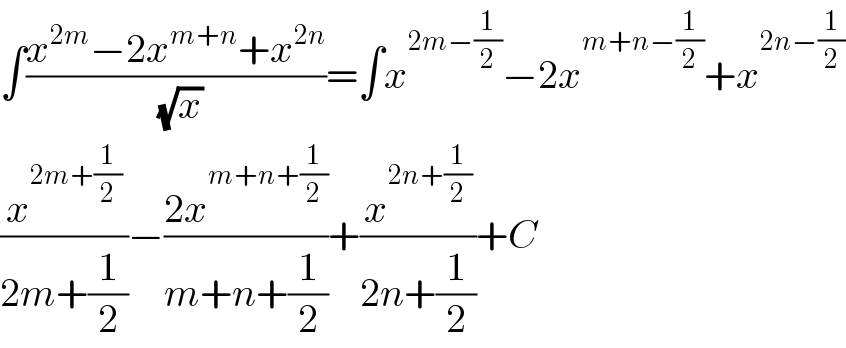
$$\int\frac{{x}^{\mathrm{2}{m}} −\mathrm{2}{x}^{{m}+{n}} +{x}^{\mathrm{2}{n}} }{\:\sqrt{{x}}}=\int{x}^{\mathrm{2}{m}−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{2}{x}^{{m}+{n}−\frac{\mathrm{1}}{\mathrm{2}}} +{x}^{\mathrm{2}{n}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\frac{{x}^{\mathrm{2}{m}+\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}{m}+\frac{\mathrm{1}}{\mathrm{2}}}−\frac{\mathrm{2}{x}^{{m}+{n}+\frac{\mathrm{1}}{\mathrm{2}}} }{{m}+{n}+\frac{\mathrm{1}}{\mathrm{2}}}+\frac{{x}^{\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{2}}}+{C} \\ $$
