Question Number 144705 by imjagoll last updated on 28/Jun/21
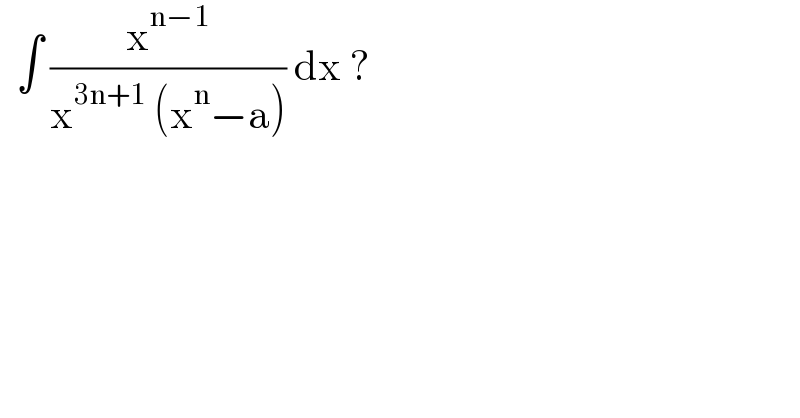
$$\:\:\int\:\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{x}^{\mathrm{3n}+\mathrm{1}} \:\left(\mathrm{x}^{\mathrm{n}} −\mathrm{a}\right)}\:\mathrm{dx}\:? \\ $$
Answered by liberty last updated on 28/Jun/21
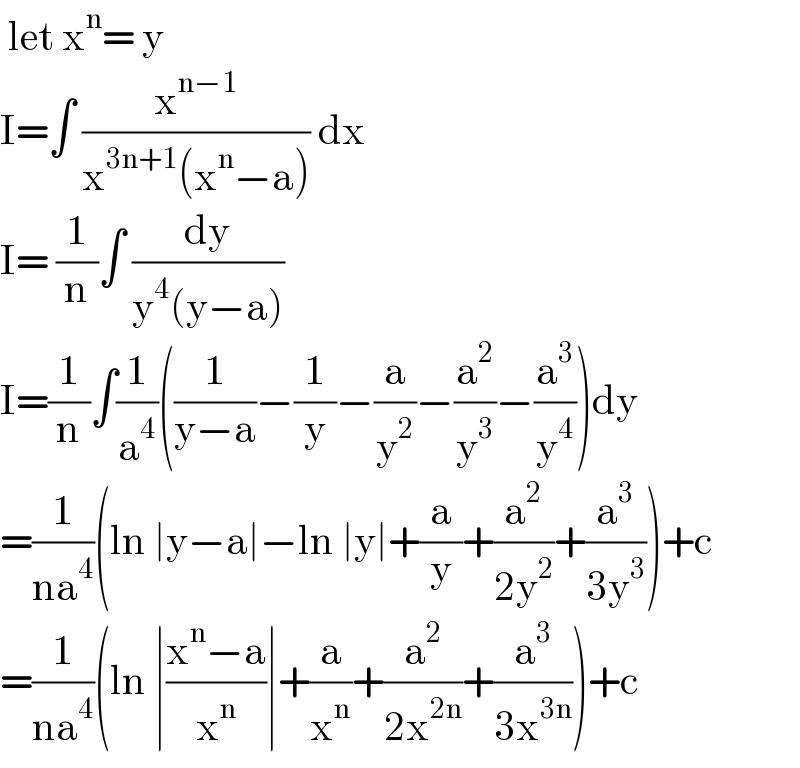
$$\:\mathrm{let}\:\mathrm{x}^{\mathrm{n}} =\:\mathrm{y} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{x}^{\mathrm{3n}+\mathrm{1}} \left(\mathrm{x}^{\mathrm{n}} −\mathrm{a}\right)}\:\mathrm{dx} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{n}}\int\:\frac{\mathrm{dy}}{\mathrm{y}^{\mathrm{4}} \left(\mathrm{y}−\mathrm{a}\right)} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{n}}\int\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{4}} }\left(\frac{\mathrm{1}}{\mathrm{y}−\mathrm{a}}−\frac{\mathrm{1}}{\mathrm{y}}−\frac{\mathrm{a}}{\mathrm{y}^{\mathrm{2}} }−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{y}^{\mathrm{3}} }−\frac{\mathrm{a}^{\mathrm{3}} }{\mathrm{y}^{\mathrm{4}} }\right)\mathrm{dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{na}^{\mathrm{4}} }\left(\mathrm{ln}\:\mid\mathrm{y}−\mathrm{a}\mid−\mathrm{ln}\:\mid\mathrm{y}\mid+\frac{\mathrm{a}}{\mathrm{y}}+\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2y}^{\mathrm{2}} }+\frac{\mathrm{a}^{\mathrm{3}} }{\mathrm{3y}^{\mathrm{3}} }\right)+\mathrm{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{na}^{\mathrm{4}} }\left(\mathrm{ln}\:\mid\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{a}}{\mathrm{x}^{\mathrm{n}} }\mid+\frac{\mathrm{a}}{\mathrm{x}^{\mathrm{n}} }+\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2x}^{\mathrm{2n}} }+\frac{\mathrm{a}^{\mathrm{3}} }{\mathrm{3x}^{\mathrm{3n}} }\right)+\mathrm{c}\: \\ $$
