x-n-cos-nx-dx-

Question Number 152186 by Tawa11 last updated on 26/Aug/21

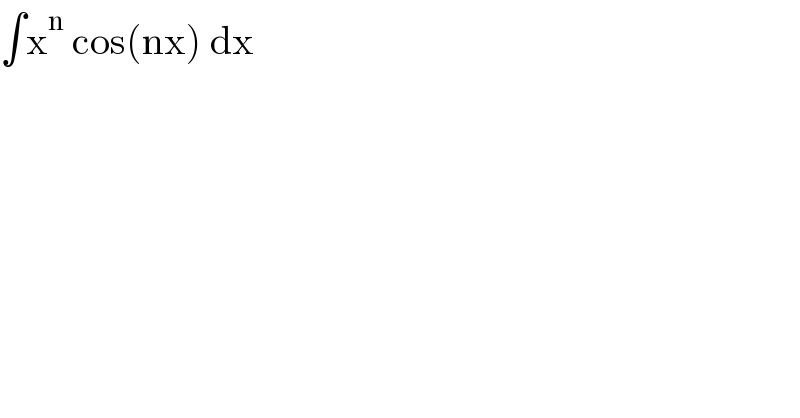
\int x^{n} \cos (nx) dx

Answered by mindispower last updated on 26/Aug/21

n x = y

\Leftrightarrow \frac{1}{n^{n + 1}} \int y^{n} c o s (x) d x

= \frac{1}{2 . n^{n + 1}} (\int y^{n} e^{i y} d y + \int y^{n} e^{- i y} d y)

i y = - t, i n f i r s t - i y = - w 2 n d \Rightarrow

= \frac{1}{2} . \frac{1}{n^{n + 1}} (i^{n + 1} \int t^{n} e^{- t} d t + {(- i)}^{n + 1} \int w^{n} e^{- w} d t)

\frac{i^{n + 1}}{2 . n^{n + 1}} \int t^{n} e^{- t} d t + \frac{{(- i)}^{n + 1}}{n^{n + 1}} \int w^{n} e^{- w} d w

r e c a l l Γ (a, x) i n c o m p l e t G a m m a f u n c t i o n

Γ (a, x) : \int_{0}^{a} t^{x - 1} e^{- t} d t

W e G e t

\frac{i^{n + 1}}{2 . n^{n + 1}} Γ (t, n + 1) + \frac{{(- i)}^{n + 1}}{2 . n^{n + 1}} Γ (w, n + 1)

= \frac{1}{2} {(\frac{i}{n})}^{n + 1} Γ (- i n x, n + 1) + \frac{1}{2} {(- \frac{i}{n})}^{n + 1} Γ (i n x, n + 1)

\int x^{n} c o s (n x) d x

= \frac{1}{2} {(\frac{i}{n})}^{n + 1} (Γ (- i n x, n + 1) + {(- 1)}^{n + 1} Γ (i n x, n + 1)) + c

Commented by Tawa11 last updated on 26/Aug/21

Thanks sir . God bless you .

Commented by mindispower last updated on 28/Aug/21

p l e a s u r s i r