Question Number 167485 by Gbenga last updated on 17/Mar/22

$$\int\int\int\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}} \boldsymbol{\mathrm{dx}} \\ $$
Answered by puissant last updated on 18/Mar/22
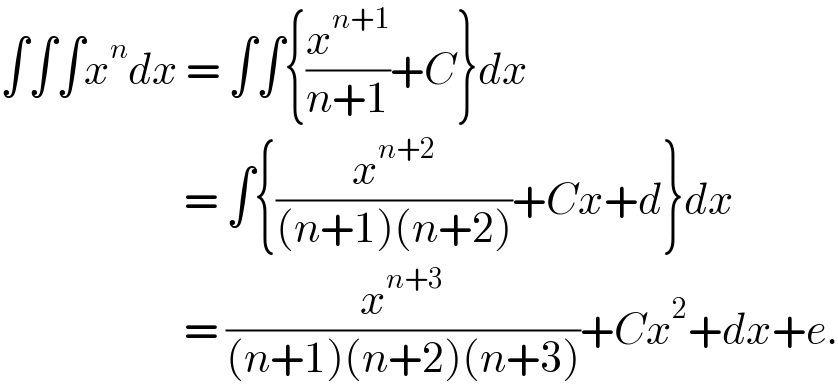
$$\int\int\int{x}^{{n}} {dx}\:=\:\int\int\left\{\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}+{C}\right\}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\int\left\{\frac{{x}^{{n}+\mathrm{2}} }{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}+{Cx}+{d}\right\}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{x}^{{n}+\mathrm{3}} }{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}+{Cx}^{\mathrm{2}} +{dx}+{e}. \\ $$
Commented by Gbenga last updated on 18/Mar/22

$${Thanks}\:{Sir} \\ $$$$ \\ $$
