Question Number 25837 by mubeen897@hotmail.com last updated on 15/Dec/17
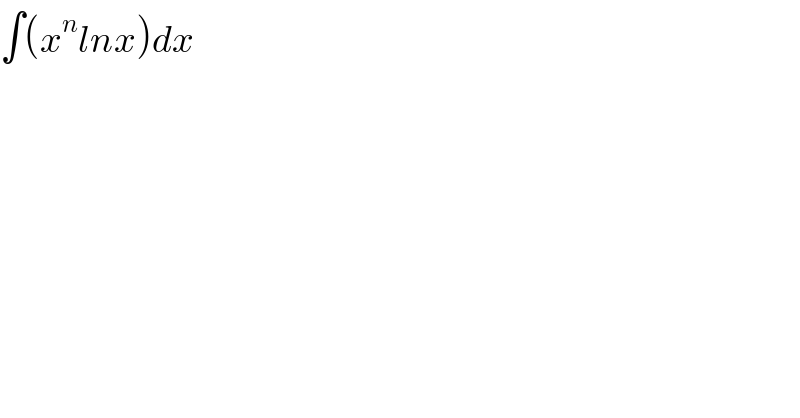
$$\int\left({x}^{{n}} {lnx}\right){dx} \\ $$
Answered by kaivan.ahmadi last updated on 15/Dec/17
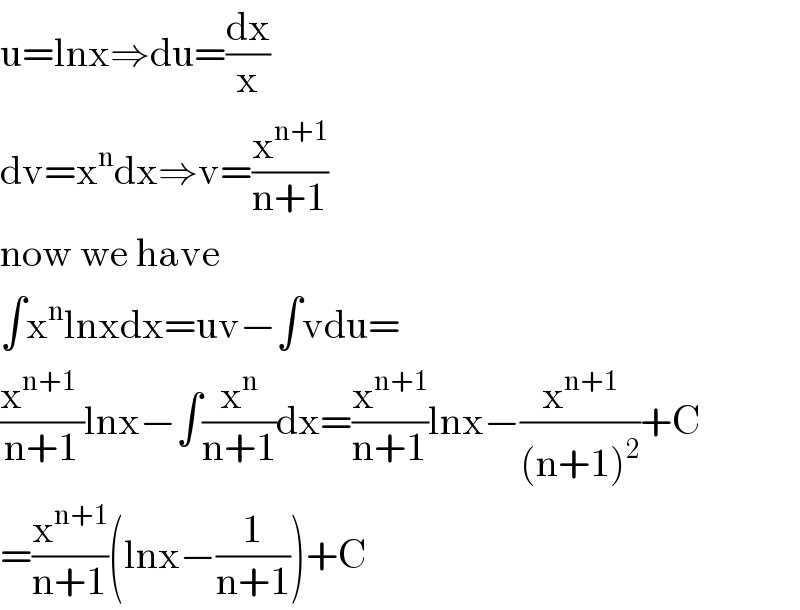
$$\mathrm{u}=\mathrm{lnx}\Rightarrow\mathrm{du}=\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$\mathrm{dv}=\mathrm{x}^{\mathrm{n}} \mathrm{dx}\Rightarrow\mathrm{v}=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\mathrm{x}^{\mathrm{n}} \mathrm{lnxdx}=\mathrm{uv}−\int\mathrm{vdu}= \\ $$$$\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} \:}{\mathrm{n}+\mathrm{1}}\mathrm{lnx}−\int\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\mathrm{dx}=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{lnx}−\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }+\mathrm{C} \\ $$$$=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\left(\mathrm{lnx}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)+\mathrm{C} \\ $$
Commented by mubeen897@hotmail.com last updated on 16/Dec/17

$${thanks}\left(−;\right. \\ $$
