Question Number 164279 by amin96 last updated on 15/Jan/22
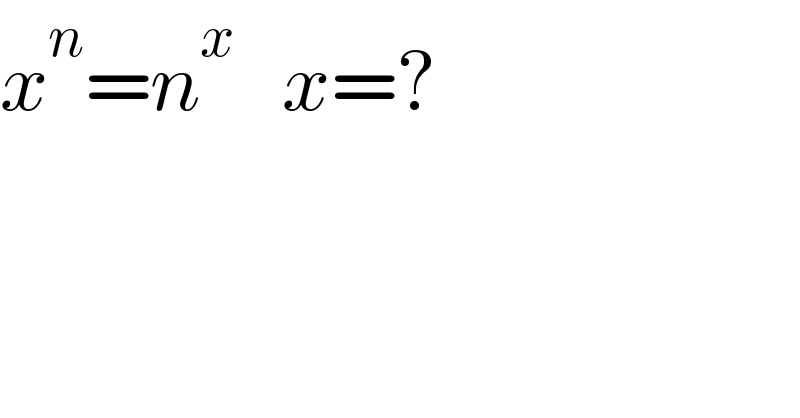
$${x}^{{n}} ={n}^{{x}} \:\:\:{x}=? \\ $$
Answered by Saiki last updated on 15/Jan/22
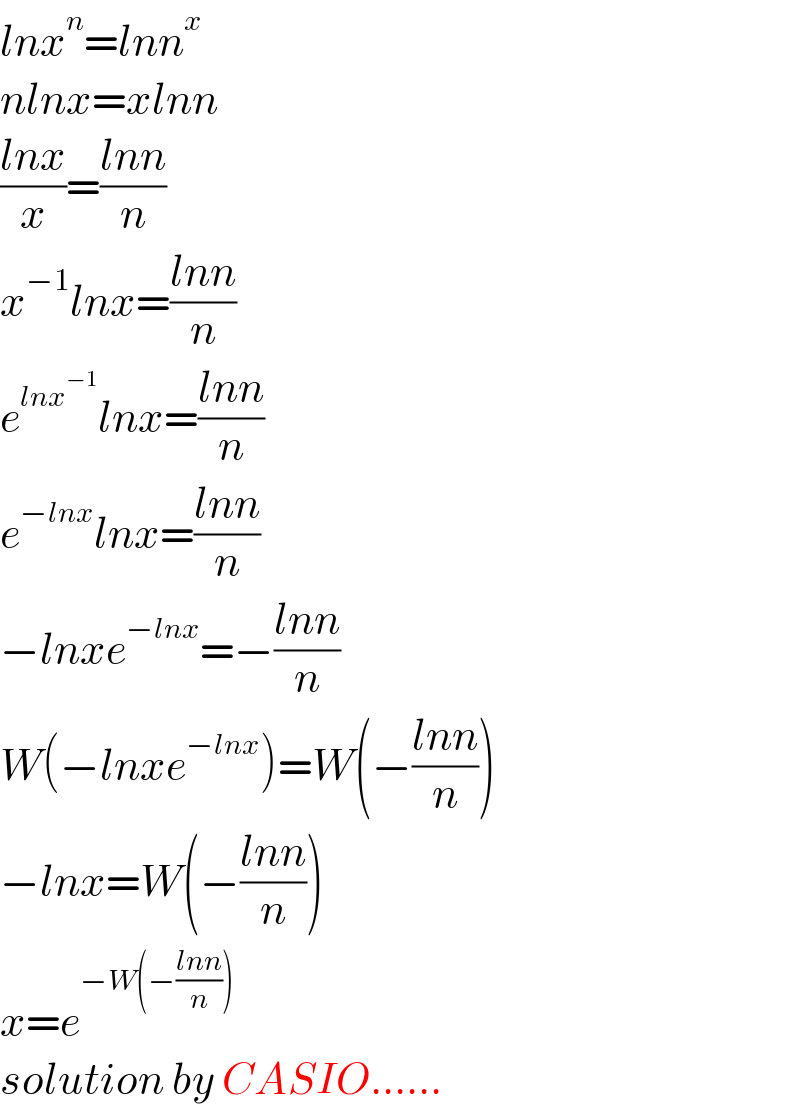
$${lnx}^{{n}} ={lnn}^{{x}} \\ $$$${nlnx}={xlnn} \\ $$$$\frac{{lnx}}{{x}}=\frac{{lnn}}{{n}} \\ $$$${x}^{−\mathrm{1}} {lnx}=\frac{{lnn}}{{n}} \\ $$$${e}^{{lnx}^{−\mathrm{1}} } {lnx}=\frac{{lnn}}{{n}} \\ $$$${e}^{−{lnx}} {lnx}=\frac{{lnn}}{{n}} \\ $$$$−{lnxe}^{−{lnx}} =−\frac{{lnn}}{{n}} \\ $$$${W}\left(−{lnxe}^{−{lnx}} \right)={W}\left(−\frac{{lnn}}{{n}}\right) \\ $$$$−{lnx}={W}\left(−\frac{{lnn}}{{n}}\right) \\ $$$${x}={e}^{−{W}\left(−\frac{{lnn}}{{n}}\right)} \\ $$$${solution}\:{by}\:{CASIO}…… \\ $$
Answered by MathsFan last updated on 15/Jan/22
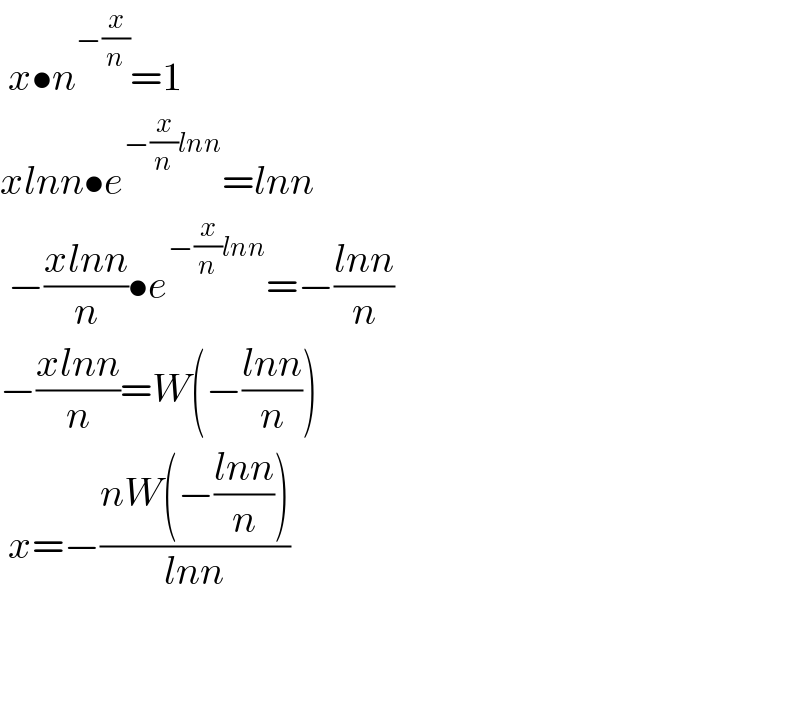
$$\:{x}\bullet{n}^{−\frac{{x}}{{n}}} =\mathrm{1} \\ $$$${xlnn}\bullet{e}^{−\frac{{x}}{{n}}{lnn}} ={lnn} \\ $$$$\:−\frac{{xlnn}}{{n}}\bullet{e}^{−\frac{{x}}{{n}}{lnn}} =−\frac{{lnn}}{{n}} \\ $$$$−\frac{{xlnn}}{{n}}={W}\left(−\frac{{lnn}}{{n}}\right) \\ $$$$\:{x}=−\frac{{nW}\left(−\frac{{lnn}}{{n}}\right)}{{lnn}} \\ $$$$ \\ $$$$\: \\ $$
Answered by mr W last updated on 15/Jan/22

$${if}\:{n}={even}\:{integer}:\:{e}.{g}.\:{x}^{\mathrm{2}} =\mathrm{2}^{{x}} \\ $$$${x}=\pm{n}^{\frac{{x}}{{n}}} \\ $$$${x}=\pm{e}^{\frac{{x}}{{n}}\mathrm{ln}\:{n}} \\ $$$$\left(−\frac{{x}}{{n}}\mathrm{ln}\:{n}\right){e}^{−\frac{{x}}{{n}}\mathrm{ln}\:{n}} =\pm\frac{\mathrm{ln}\:{n}}{{n}} \\ $$$$\left(−\frac{{x}}{{n}}\mathrm{ln}\:{n}\right)={W}\left(\pm\frac{\mathrm{ln}\:{n}}{{n}}\right) \\ $$$$\Rightarrow{x}=−\frac{{n}}{\mathrm{ln}\:{n}}{W}\left(\pm\frac{\mathrm{ln}\:{n}}{{n}}\right) \\ $$$${similarly},\:{if}\:{n}\neq{even}\:{integer},\:{e}.{g}.\:{x}^{\mathrm{3}} =\mathrm{3}^{{x}} : \\ $$$$\Rightarrow{x}=−\frac{{n}}{\mathrm{ln}\:{n}}{W}\left(−\frac{\mathrm{ln}\:{n}}{{n}}\right) \\ $$
