Question Number 119015 by benjo_mathlover last updated on 21/Oct/20

$${x}\:=\:\frac{\mathrm{sin}\:\mathrm{1}°+\mathrm{sin}\:\mathrm{2}°+\mathrm{sin}\:\mathrm{3}°+…+\mathrm{sin}\:\mathrm{45}°}{\mathrm{cos}\:\mathrm{1}°+\mathrm{cos}\:\mathrm{2}°+\mathrm{cos}\:\mathrm{3}°+…+\mathrm{cos}\:\mathrm{45}°} \\ $$$${x}\:=\:? \\ $$
Commented by Dwaipayan Shikari last updated on 21/Oct/20
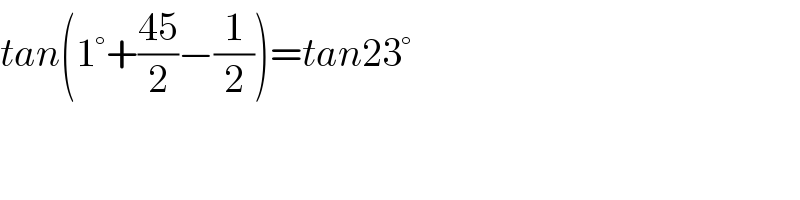
$${tan}\left(\mathrm{1}°+\frac{\mathrm{45}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\right)={tan}\mathrm{23}° \\ $$
Answered by Dwaipayan Shikari last updated on 21/Oct/20
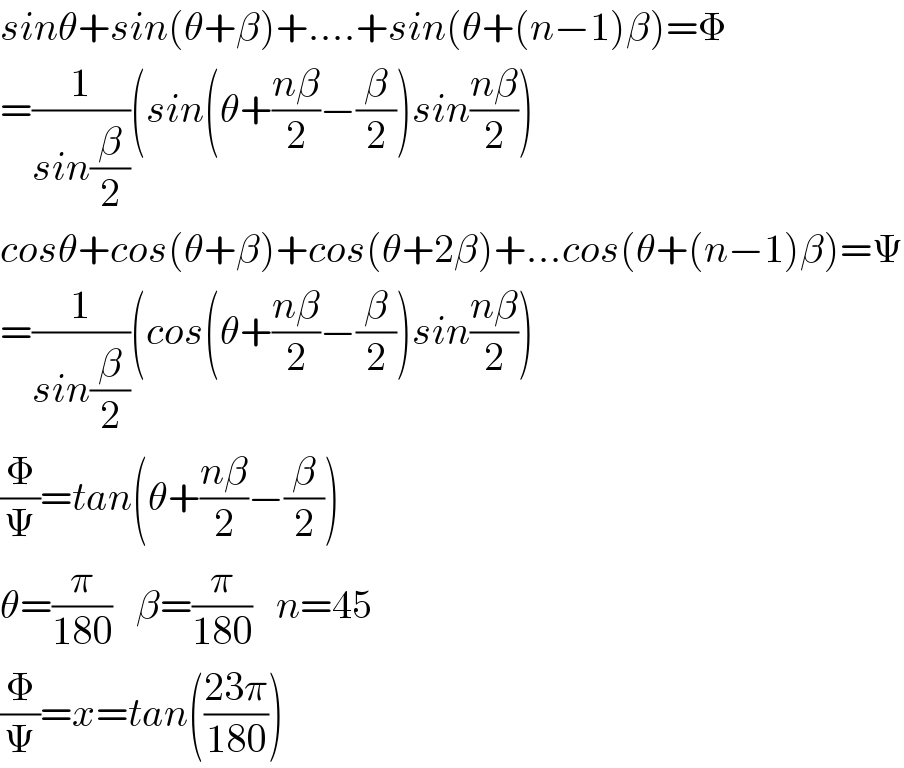
$${sin}\theta+{sin}\left(\theta+\beta\right)+….+{sin}\left(\theta+\left({n}−\mathrm{1}\right)\beta\right)=\Phi \\ $$$$=\frac{\mathrm{1}}{{sin}\frac{\beta}{\mathrm{2}}}\left({sin}\left(\theta+\frac{{n}\beta}{\mathrm{2}}−\frac{\beta}{\mathrm{2}}\right){sin}\frac{{n}\beta}{\mathrm{2}}\right) \\ $$$${cos}\theta+{cos}\left(\theta+\beta\right)+{cos}\left(\theta+\mathrm{2}\beta\right)+…{cos}\left(\theta+\left({n}−\mathrm{1}\right)\beta\right)=\Psi \\ $$$$=\frac{\mathrm{1}}{{sin}\frac{\beta}{\mathrm{2}}}\left({cos}\left(\theta+\frac{{n}\beta}{\mathrm{2}}−\frac{\beta}{\mathrm{2}}\right){sin}\frac{{n}\beta}{\mathrm{2}}\right) \\ $$$$\frac{\Phi}{\Psi}={tan}\left(\theta+\frac{{n}\beta}{\mathrm{2}}−\frac{\beta}{\mathrm{2}}\right) \\ $$$$\theta=\frac{\pi}{\mathrm{180}}\:\:\:\beta=\frac{\pi}{\mathrm{180}}\:\:\:{n}=\mathrm{45} \\ $$$$\frac{\Phi}{\Psi}={x}={tan}\left(\frac{\mathrm{23}\pi}{\mathrm{180}}\right) \\ $$
