Menu Close

x-sin-2-x-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 102198 by Study last updated on 07/Jul/20
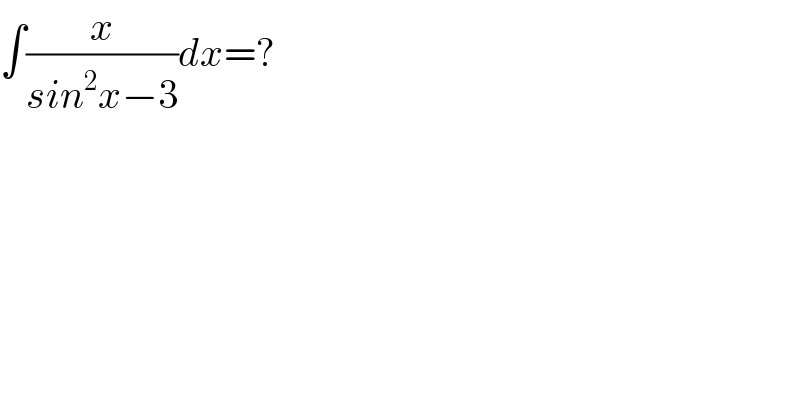
∫(x/(sin^2 x−3))dx=?
$$\int\frac{{x}}{{sin}^{\mathrm{2}} {x}−\mathrm{3}}{dx}=? \\ $$
Answered by mathmax by abdo last updated on 08/Jul/20
not resoluble(√!)
$$\mathrm{not}\:\mathrm{resoluble}\sqrt{!} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Jul/20
∫(x/((sinx+(√3))(sinx−(√3)))) (x/(2(√3)))∫(1/(sinx−(√3)))−(1/(sinx−(√3)))dx−∫(∫(1/(sin^2 x−3)))dx x(1/(2(√3)))(I_a −I_b )−∫(∫(1/(sin^2 x−3)))dx I_a =∫(1/(sinx−(√3)))dx =2∫(dt/((((2t)/(t^2 +1))−(√3))(t^2 +1)))=2∫(1/(2t−(√3)t^2 −(√3)))dt=−(2/( (√3)))∫(1/(t^2 −((2t)/( (√3)))+1)) =−(2/( (√3)))∫(1/((t−(1/( (√3))))^2 +((√(2/3)))^2 ))dt =−(1/( (√2)))tan^(−1) (((√3)t−1)/( (√2))) =−(1/( (√2)))tan^(−1) (((√3)tan(x/2)−1)/( (√2))) I_b =∫(1/(sinx+(√3)))=2∫(1/((((2t)/(t^2 +1))+(√3))(t^2 +1)))dt =(2/( (√3)))∫(1/(t^2 +((2t)/( (√3)))+1))=(1/( (√2)))tan^(−1) (((√3)tan(x/2)+1)/( (√2))) (x/(2(√3)))(I_a −I_b )=−(x/(2(√6)))(tan^(−1) (((√3)tan(x/2)+1)/( (√2)))+tan^(−1) (((√3)tan(x/2)−1)/( (√2)))).... .....continue But now we have to integrate ∫(I_a −I_b )= −∫tan^(−1) ((((2(√3)tan(x/2))/( (√2)))/(1−((3tan^2 (x/2)−1)/2)))) −∫tan^(−1) (((2(√6)tan(x/2))/(1−3tan^2 (x/2))))........continue =−xtan^(−1) (((2(√6)tan(x/2))/(1−3tan^2 (x/2))))+∫((x(√6)sec^2 (x/2))/(1+9tan^4 (x/2)+18tan^2 (x/2))) (x/(−2(√3)))(I_a −I_b )−∫(I_a −I_b ) =−(((x+1))/(2(√6)))(tan^(−1) (((2(√6)tan(x/2))/(1−3tan^2 (x/2)))))+∫((x(√6)sec^2 (x/2))/(1+9tan^4 (x/2)+18tan^2 (x/2)))+Constant
$$\int\frac{{x}}{\left({sinx}+\sqrt{\mathrm{3}}\right)\left({sinx}−\sqrt{\mathrm{3}}\right)} \\ $$$$\frac{{x}}{\mathrm{2}\sqrt{\mathrm{3}}}\int\frac{\mathrm{1}}{{sinx}−\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{{sinx}−\sqrt{\mathrm{3}}}{dx}−\int\left(\int\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {x}−\mathrm{3}}\right){dx} \\ $$$${x}\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left({I}_{{a}} −{I}_{{b}} \right)−\int\left(\int\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {x}−\mathrm{3}}\right){dx} \\ $$$${I}_{{a}} =\int\frac{\mathrm{1}}{{sinx}−\sqrt{\mathrm{3}}}{dx} \\ $$$$\:\:\:\:=\mathrm{2}\int\frac{{dt}}{\left(\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}−\sqrt{\mathrm{3}}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}=\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{2}{t}−\sqrt{\mathrm{3}}{t}^{\mathrm{2}} −\sqrt{\mathrm{3}}}{dt}=−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} −\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{3}}}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\int\frac{\mathrm{1}}{\left({t}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\right)^{\mathrm{2}} }{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}{t}−\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}{tan}\frac{{x}}{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${I}_{{b}} =\int\frac{\mathrm{1}}{{sinx}+\sqrt{\mathrm{3}}}=\mathrm{2}\int\frac{\mathrm{1}}{\left(\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}+\sqrt{\mathrm{3}}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{dt} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{3}}}+\mathrm{1}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}{tan}\frac{{x}}{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\frac{{x}}{\mathrm{2}\sqrt{\mathrm{3}}}\left({I}_{{a}} −{I}_{{b}} \right)=−\frac{{x}}{\mathrm{2}\sqrt{\mathrm{6}}}\left({tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}{tan}\frac{{x}}{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}}+{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}{tan}\frac{{x}}{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)…. \\ $$$$…..{continue} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${But}\:{now}\:{we}\:{have}\:{to}\:{integrate} \\ $$$$\int\left({I}_{{a}} −{I}_{{b}} \right)=\:−\int{tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{2}\sqrt{\mathrm{3}}{tan}\frac{{x}}{\mathrm{2}}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}−\frac{\mathrm{3}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{1}}{\mathrm{2}}}\right) \\ $$$$−\int{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{6}}{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{1}−\mathrm{3}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}\right)……..{continue} \\ $$$$=−{xtan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{6}}{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{1}−\mathrm{3}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}\right)+\int\frac{{x}\sqrt{\mathrm{6}}{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{9}{tan}^{\mathrm{4}} \frac{{x}}{\mathrm{2}}+\mathrm{18}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$$$ \\ $$$$ \\ $$$$\frac{{x}}{−\mathrm{2}\sqrt{\mathrm{3}}}\left({I}_{{a}} −{I}_{{b}} \right)−\int\left({I}_{{a}} −{I}_{{b}} \right) \\ $$$$=−\frac{\left({x}+\mathrm{1}\right)}{\mathrm{2}\sqrt{\mathrm{6}}}\left({tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{6}}{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{1}−\mathrm{3}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}\right)\right)+\int\frac{{x}\sqrt{\mathrm{6}}{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{9}{tan}^{\mathrm{4}} \frac{{x}}{\mathrm{2}}+\mathrm{18}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}+{Constant} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *