Question Number 112847 by bemath last updated on 10/Sep/20
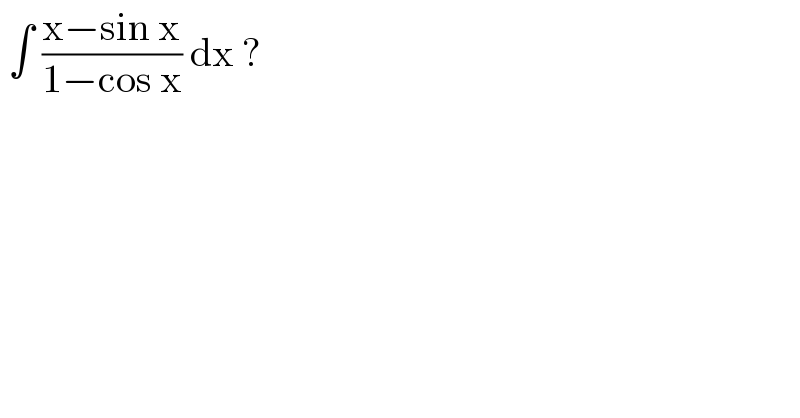
$$\:\int\:\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\:? \\ $$
Answered by bobhans last updated on 10/Sep/20
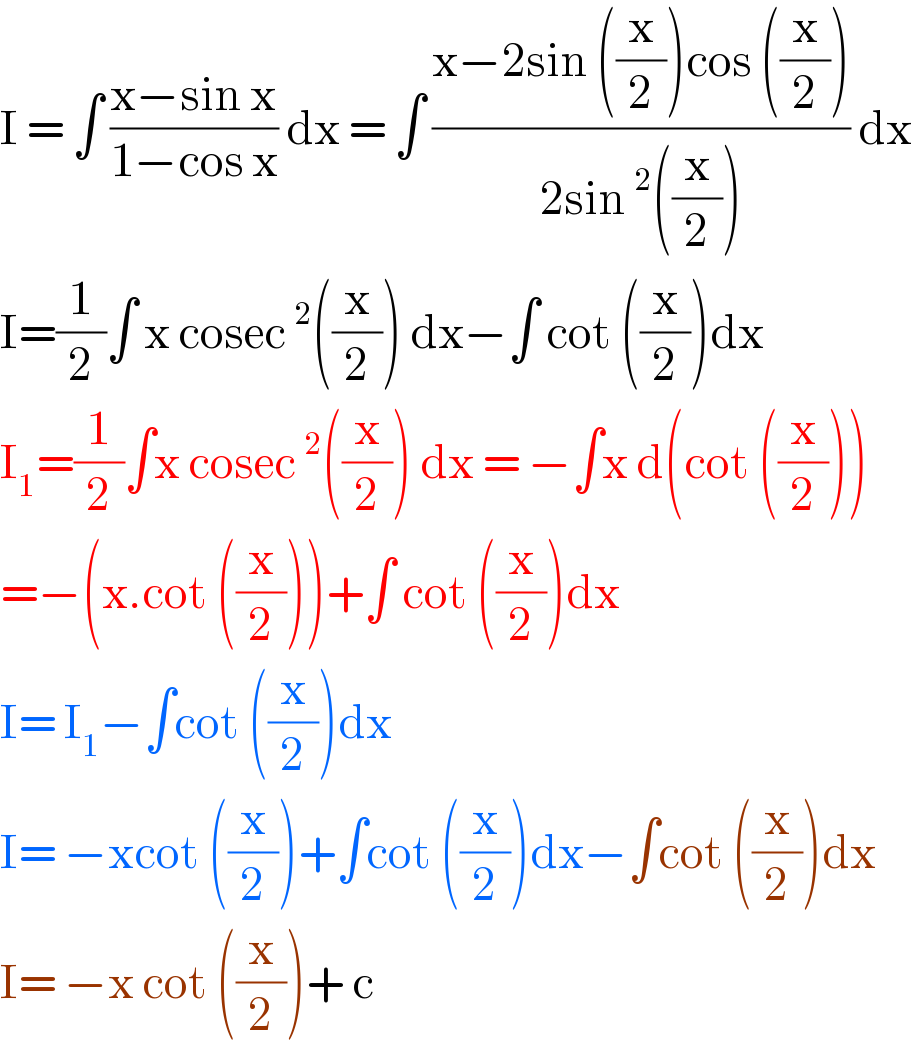
$$\mathrm{I}\:=\:\int\:\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\:=\:\int\:\frac{\mathrm{x}−\mathrm{2sin}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)}\:\mathrm{dx} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{x}\:\mathrm{cosec}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:\mathrm{dx}−\int\:\mathrm{cot}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{x}\:\mathrm{cosec}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:\mathrm{dx}\:=\:−\int\mathrm{x}\:\mathrm{d}\left(\mathrm{cot}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right) \\ $$$$=−\left(\mathrm{x}.\mathrm{cot}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)+\int\:\mathrm{cot}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx} \\ $$$$\mathrm{I}=\:\mathrm{I}_{\mathrm{1}} −\int\mathrm{cot}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx}\: \\ $$$$\mathrm{I}=\:−\mathrm{xcot}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\int\mathrm{cot}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx}−\int\mathrm{cot}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx} \\ $$$$\mathrm{I}=\:−\mathrm{x}\:\mathrm{cot}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\:\mathrm{c} \\ $$
Commented by bemath last updated on 10/Sep/20

$$\mathrm{santuuuyyy} \\ $$
