Question Number 42364 by Tawa1 last updated on 24/Aug/18
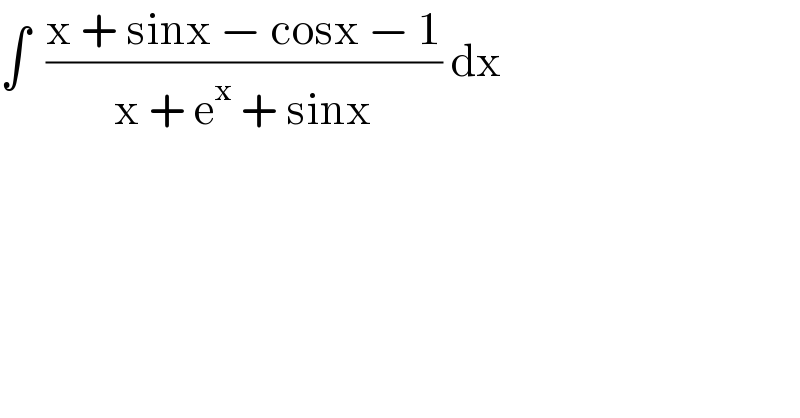
$$\int\:\:\frac{\mathrm{x}\:+\:\mathrm{sinx}\:−\:\mathrm{cosx}\:−\:\mathrm{1}}{\mathrm{x}\:+\:\mathrm{e}^{\mathrm{x}} \:+\:\mathrm{sinx}}\:\mathrm{dx} \\ $$
Commented by maxmathsup by imad last updated on 24/Aug/18
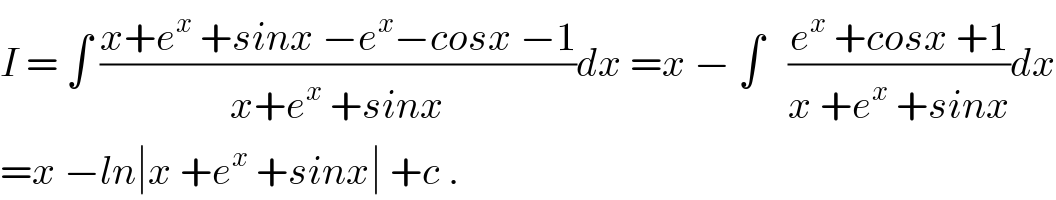
$${I}\:=\:\int\:\frac{{x}+{e}^{{x}} \:+{sinx}\:−{e}^{{x}} −{cosx}\:−\mathrm{1}}{{x}+{e}^{{x}} \:+{sinx}}{dx}\:={x}\:−\:\int\:\:\:\frac{{e}^{{x}} \:+{cosx}\:+\mathrm{1}}{{x}\:+{e}^{{x}} \:+{sinx}}{dx} \\ $$$$={x}\:−{ln}\mid{x}\:+{e}^{{x}} \:+{sinx}\mid\:+{c}\:. \\ $$
Commented by maxmathsup by imad last updated on 24/Aug/18

$${nevermind}\:{sir}. \\ $$
Commented by Tawa1 last updated on 24/Aug/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
