Menu Close

x-t-1-y-2t-3-z-t-2-x-3t-2-y-t-1-z-t-1-Are-these-two-lines-located-in-the-same-plane-or-not-where-t-R-

Tinku Tara 0 Comments
Pin




Question Number 182772 by Acem last updated on 14/Dec/22
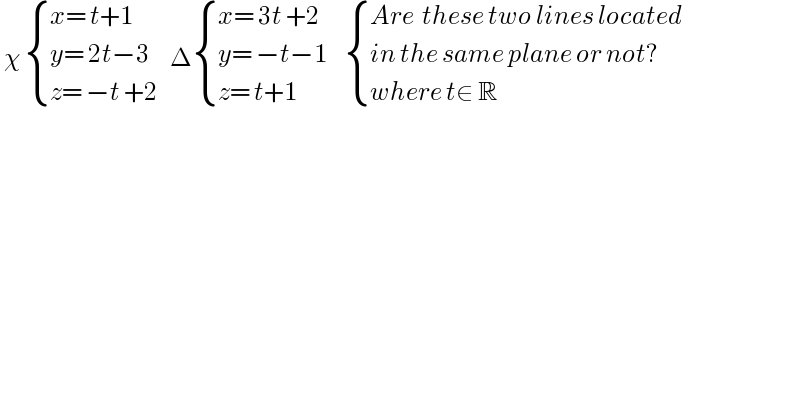
χ { ((x= t+1)),((y= 2t−3)),((z= −t +2)) :} Δ { ((x= 3t +2)),((y= −t−1 )),((z= t+1)) :} { ((Are these two lines located)),((in the same plane or not?)),((where t∈ R)) :}
$$\:\chi\:\begin{cases}{{x}=\:{t}+\mathrm{1}}\\{{y}=\:\mathrm{2}{t}−\mathrm{3}}\\{{z}=\:−{t}\:+\mathrm{2}}\end{cases}\:\:\:\Delta\begin{cases}{{x}=\:\mathrm{3}{t}\:+\mathrm{2}}\\{{y}=\:−{t}−\mathrm{1}\:\:\:}\\{{z}=\:{t}+\mathrm{1}}\end{cases}\:\begin{cases}{{Are}\:\:{these}\:{two}\:{lines}\:{located}}\\{{in}\:{the}\:{same}\:{plane}\:{or}\:{not}?}\\{{where}\:{t}\in\:\mathbb{R}}\end{cases} \\ $$$$ \\ $$
Answered by mr W last updated on 14/Dec/22
Method I line 1: (1,−3,2)+s(1,2,−1) line 2: (2,−1,1)+t(3,−1,1) it′s to see that both lines are not parallel. assume they lie in the same plane, then they should intersect. 1+s=2+3t ...(i) −3+2s=−1−t ...(ii) 2−s=1+t ...(iii) from (i) and (iii): ⇒t=0, s=1 put this into (ii): −3+2=−1−0 ✓ that means both lines intersect indeed. they lie in the same plane.
$${Method}\:{I} \\ $$$${line}\:\mathrm{1}:\:\left(\mathrm{1},−\mathrm{3},\mathrm{2}\right)+{s}\left(\mathrm{1},\mathrm{2},−\mathrm{1}\right) \\ $$$${line}\:\mathrm{2}:\:\left(\mathrm{2},−\mathrm{1},\mathrm{1}\right)+{t}\left(\mathrm{3},−\mathrm{1},\mathrm{1}\right) \\ $$$${it}'{s}\:{to}\:{see}\:{that}\:{both}\:{lines}\:{are}\:{not}\: \\ $$$${parallel}. \\ $$$${assume}\:{they}\:{lie}\:{in}\:{the}\:{same}\:{plane}, \\ $$$${then}\:{they}\:{should}\:{intersect}. \\ $$$$\mathrm{1}+{s}=\mathrm{2}+\mathrm{3}{t}\:\:\:\:\:\:…\left({i}\right) \\ $$$$−\mathrm{3}+\mathrm{2}{s}=−\mathrm{1}−{t}\:\:\:\:…\left({ii}\right) \\ $$$$\mathrm{2}−{s}=\mathrm{1}+{t}\:\:\:\:…\left({iii}\right) \\ $$$${from}\:\left({i}\right)\:{and}\:\left({iii}\right): \\ $$$$\Rightarrow{t}=\mathrm{0},\:{s}=\mathrm{1} \\ $$$${put}\:{this}\:{into}\:\left({ii}\right): \\ $$$$−\mathrm{3}+\mathrm{2}=−\mathrm{1}−\mathrm{0}\:\checkmark \\ $$$${that}\:{means}\:{both}\:{lines}\:{intersect}\:{indeed}. \\ $$$${they}\:{lie}\:{in}\:{the}\:{same}\:{plane}. \\ $$
Commented by mr W last updated on 14/Dec/22
Method II vector 1: (1,2,−1) vector 2: (3,−1,1) vector 3: (1,2,−1) =PQ^(→) ∗) n_1 =v_1 ×v_3 =(0,0,0) n_2 =v_2 ×v_3 =(−1,4,7) n_1 // n_2 . the lines are coplanar. ∗) it′s to see that point Q on line 2 lies also on line 1, both lines are in the same plane.
$${Method}\:{II} \\ $$$${vector}\:\mathrm{1}:\:\left(\mathrm{1},\mathrm{2},−\mathrm{1}\right) \\ $$$${vector}\:\mathrm{2}:\:\left(\mathrm{3},−\mathrm{1},\mathrm{1}\right) \\ $$$$\left.{vector}\:\mathrm{3}:\:\left(\mathrm{1},\mathrm{2},−\mathrm{1}\right)\:=\overset{\rightarrow} {{PQ}}\:\:\:\:\ast\right) \\ $$$${n}_{\mathrm{1}} =\mathrm{v}_{\mathrm{1}} ×\mathrm{v}_{\mathrm{3}} =\left(\mathrm{0},\mathrm{0},\mathrm{0}\right) \\ $$$${n}_{\mathrm{2}} =\mathrm{v}_{\mathrm{2}} ×\mathrm{v}_{\mathrm{3}} =\left(−\mathrm{1},\mathrm{4},\mathrm{7}\right) \\ $$$${n}_{\mathrm{1}} \://\:{n}_{\mathrm{2}} .\:{the}\:{lines}\:{are}\:{coplanar}. \\ $$$$ \\ $$$$\left.\ast\right)\:{it}'{s}\:{to}\:{see}\:{that}\:{point}\:{Q}\:{on}\:{line}\:\mathrm{2} \\ $$$${lies}\:{also}\:{on}\:{line}\:\mathrm{1},\:{both}\:{lines}\:{are}\:{in} \\ $$$${the}\:{same}\:{plane}. \\ $$
Commented by Acem last updated on 14/Dec/22
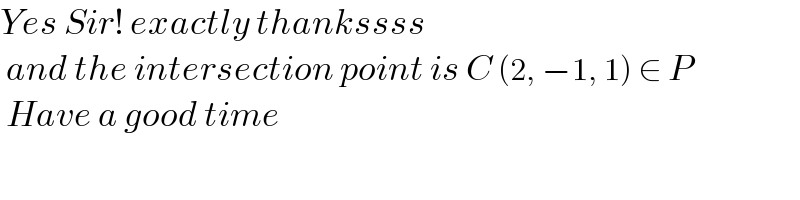
Yes Sir! exactly thankssss and the intersection point is C (2, −1, 1) ∈ P Have a good time
$${Yes}\:{Sir}!\:{exactly}\:{thankssss} \\ $$$$\:{and}\:{the}\:{intersection}\:{point}\:{is}\:{C}\:\left(\mathrm{2},\:−\mathrm{1},\:\mathrm{1}\right)\:\in\:{P} \\ $$$$\:{Have}\:{a}\:{good}\:{time} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *