Question Number 81636 by jagoll last updated on 14/Feb/20
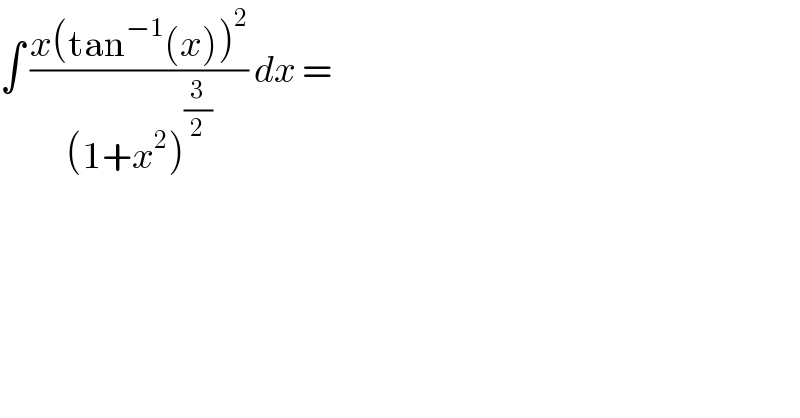
$$\int\:\frac{{x}\left(\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:{dx}\:=\: \\ $$
Commented by mind is power last updated on 14/Feb/20
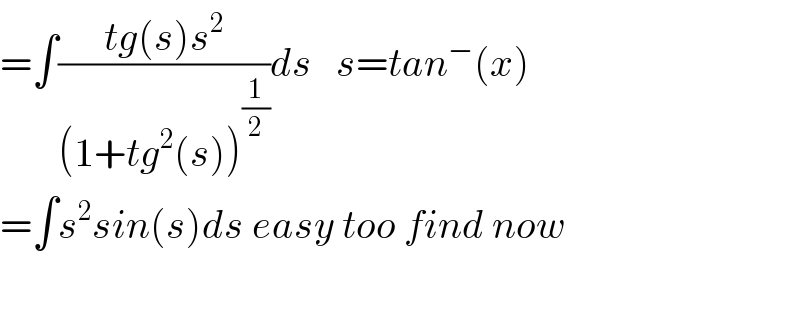
$$=\int\frac{{tg}\left({s}\right){s}^{\mathrm{2}} }{\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({s}\right)\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{ds}\:\:\:{s}={tan}^{−} \left({x}\right) \\ $$$$=\int{s}^{\mathrm{2}} {sin}\left({s}\right){ds}\:{easy}\:{too}\:{find}\:{now} \\ $$$$ \\ $$
Commented by jagoll last updated on 14/Feb/20
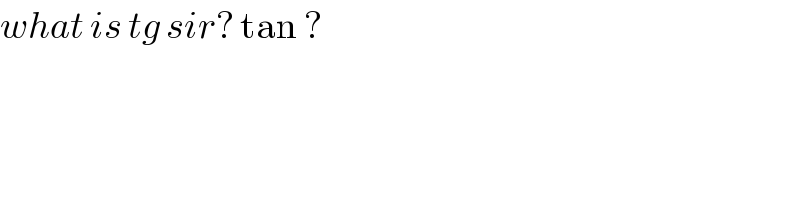
$${what}\:{is}\:{tg}\:{sir}?\:\mathrm{tan}\:? \\ $$
Commented by peter frank last updated on 14/Feb/20
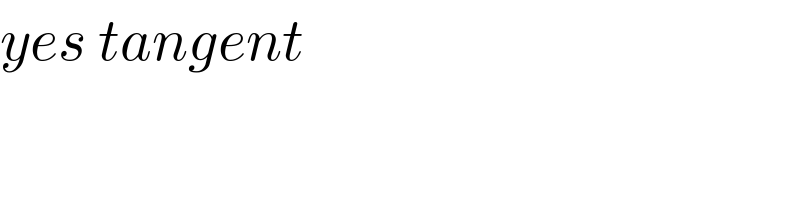
$${yes}\:{tangent} \\ $$
Commented by mathmax by abdo last updated on 14/Feb/20
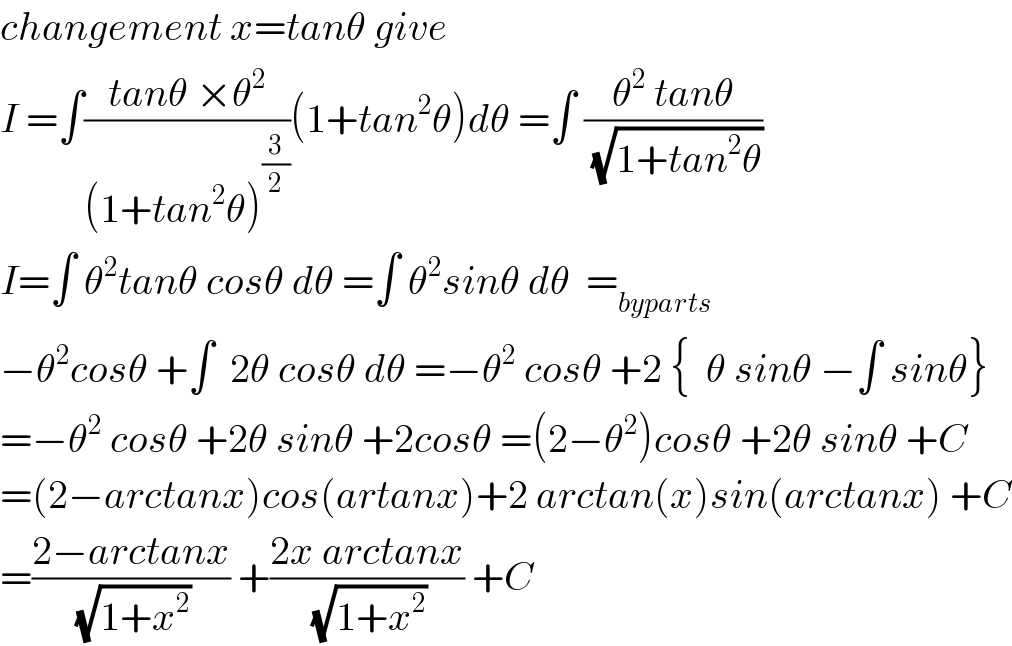
$${changement}\:{x}={tan}\theta\:{give}\: \\ $$$${I}\:=\int\frac{{tan}\theta\:×\theta^{\mathrm{2}} }{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta\:=\int\:\frac{\theta^{\mathrm{2}} \:{tan}\theta}{\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}} \\ $$$${I}=\int\:\theta^{\mathrm{2}} {tan}\theta\:{cos}\theta\:{d}\theta\:=\int\:\theta^{\mathrm{2}} {sin}\theta\:{d}\theta\:\:=_{{byparts}} \\ $$$$−\theta^{\mathrm{2}} {cos}\theta\:+\int\:\:\mathrm{2}\theta\:{cos}\theta\:{d}\theta\:=−\theta^{\mathrm{2}} \:{cos}\theta\:+\mathrm{2}\:\left\{\:\:\theta\:{sin}\theta\:−\int\:{sin}\theta\right\} \\ $$$$=−\theta^{\mathrm{2}} \:{cos}\theta\:+\mathrm{2}\theta\:{sin}\theta\:+\mathrm{2}{cos}\theta\:=\left(\mathrm{2}−\theta^{\mathrm{2}} \right){cos}\theta\:+\mathrm{2}\theta\:{sin}\theta\:+{C} \\ $$$$=\left(\mathrm{2}−{arctanx}\right){cos}\left({artanx}\right)+\mathrm{2}\:{arctan}\left({x}\right){sin}\left({arctanx}\right)\:+{C} \\ $$$$=\frac{\mathrm{2}−{arctanx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:+\frac{\mathrm{2}{x}\:{arctanx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:+{C} \\ $$
