Question Number 63261 by aliesam last updated on 01/Jul/19
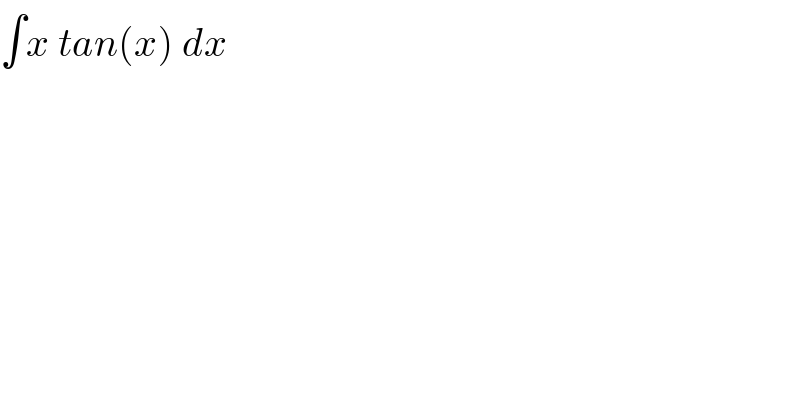
$$\int{x}\:{tan}\left({x}\right)\:{dx} \\ $$
Commented by kaivan.ahmadi last updated on 01/Jul/19
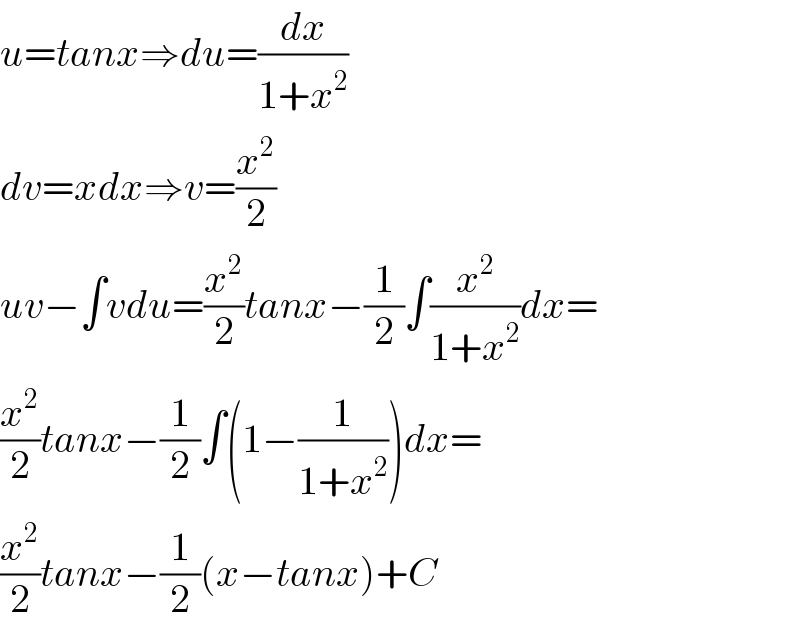
$${u}={tanx}\Rightarrow{du}=\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${dv}={xdx}\Rightarrow{v}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${uv}−\int{vdu}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{tanx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}= \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{tanx}−\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx}= \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{tanx}−\frac{\mathrm{1}}{\mathrm{2}}\left({x}−{tanx}\right)+{C} \\ $$
Commented by aliesam last updated on 01/Jul/19

$${well}\:{done}\:{sir}\: \\ $$
Commented by aliesam last updated on 01/Jul/19
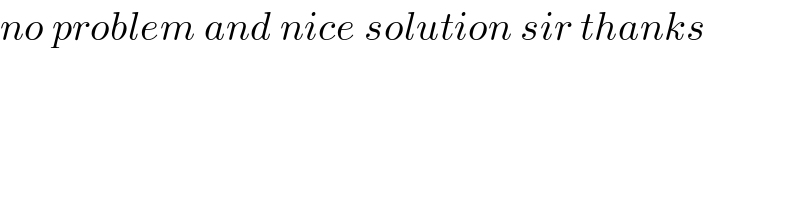
$${no}\:{problem}\:{and}\:{nice}\:{solution}\:{sir}\:{thanks} \\ $$
Commented by mathmax by abdo last updated on 01/Jul/19
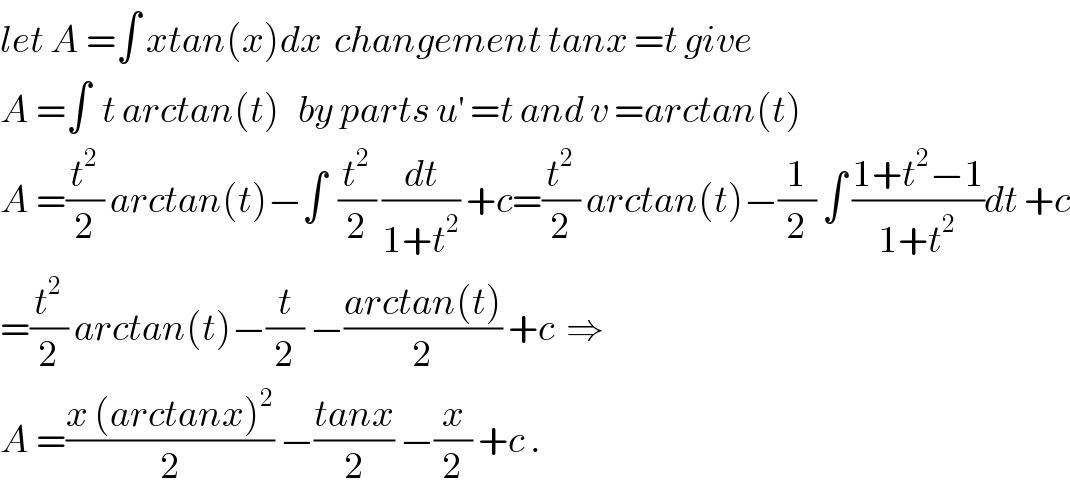
$${let}\:{A}\:=\int\:{xtan}\left({x}\right){dx}\:\:{changement}\:{tanx}\:={t}\:{give} \\ $$$${A}\:=\int\:\:{t}\:{arctan}\left({t}\right)\:\:\:{by}\:{parts}\:{u}^{'} \:={t}\:{and}\:{v}\:={arctan}\left({t}\right)\: \\ $$$${A}\:=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:{arctan}\left({t}\right)−\int\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:+{c}=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:{arctan}\left({t}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:+{c} \\ $$$$=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:{arctan}\left({t}\right)−\frac{{t}}{\mathrm{2}}\:−\frac{{arctan}\left({t}\right)}{\mathrm{2}}\:+{c}\:\:\Rightarrow \\ $$$${A}\:=\frac{{x}\:\left({arctanx}\right)^{\mathrm{2}} }{\mathrm{2}}\:−\frac{{tanx}}{\mathrm{2}}\:−\frac{{x}}{\mathrm{2}}\:+{c}\:. \\ $$
Commented by mathmax by abdo last updated on 01/Jul/19
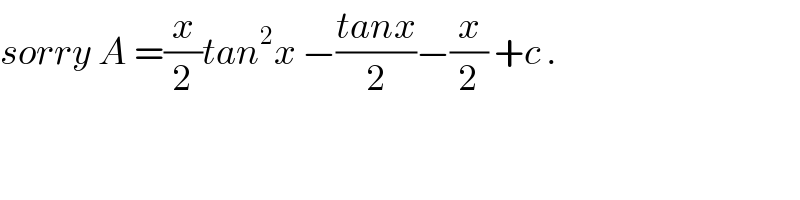
$${sorry}\:{A}\:=\frac{{x}}{\mathrm{2}}{tan}^{\mathrm{2}} {x}\:−\frac{{tanx}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\:+{c}\:. \\ $$
Commented by mathmax by abdo last updated on 02/Jul/19

$${you}\:{are}\:{welcome}. \\ $$
