Question Number 85832 by jagoll last updated on 25/Mar/20
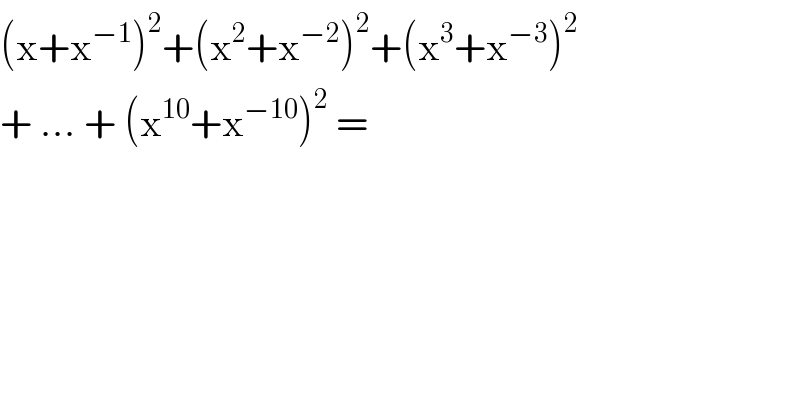
$$\left(\mathrm{x}+\mathrm{x}^{−\mathrm{1}} \right)^{\mathrm{2}} +\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{−\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{−\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$+\:…\:+\:\left(\mathrm{x}^{\mathrm{10}} +\mathrm{x}^{−\mathrm{10}} \right)^{\mathrm{2}} \:=\: \\ $$
Commented by mathmax by abdo last updated on 25/Mar/20

$${let}\:{A}_{{n}} \left({x}\right)=\left({x}+{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \:+\left({x}^{\mathrm{2}} \:+{x}^{−\mathrm{2}} \right)^{\mathrm{2}} \:+\left({x}^{\mathrm{3}} \:+{x}^{−\mathrm{3}} \right)^{\mathrm{2}} +…+\left({x}^{{n}} \:+{x}^{−{n}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow{A}_{{n}} ={x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\mathrm{2}\:\:+{x}^{\mathrm{4}} \:+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:+\mathrm{2}\:+….{x}^{\mathrm{2}{n}} \:+\frac{\mathrm{1}}{{x}^{\mathrm{2}{n}} }\:+\mathrm{2} \\ $$$$={x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} \:+….+{x}^{\mathrm{2}{n}} \:+\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} \:+\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{4}} \:+….+\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}{n}} \:+\mathrm{2}{n} \\ $$$$={w}\left({x}\right)+{w}\left(\frac{\mathrm{1}}{{x}}\right)\:+\mathrm{2}{n}\:{with}\:{w}\left({x}\right)={x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} \:+…{x}^{\mathrm{2}{n}} \\ $$$$={x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \:+…+\left({x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} \right)\:={x}^{\mathrm{2}} ×\frac{\mathrm{1}−\left({x}^{\mathrm{2}} \right)^{{n}} }{\mathrm{1}−{x}^{\mathrm{2}} }\:=\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }\left(\mathrm{1}−{x}^{\mathrm{2}{n}} \right) \\ $$$${w}\left(\frac{\mathrm{1}}{{x}}\right)\:=\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}{n}} }\right)\:=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}{n}} }\right)\:=\frac{{x}^{\mathrm{2}{n}} −\mathrm{1}}{{x}^{\mathrm{2}{n}+\mathrm{2}} }\:\Rightarrow \\ $$$${A}_{{n}} \left({x}\right)=\frac{{x}^{\mathrm{2}} −{x}^{\mathrm{2}{n}+\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }\:+\frac{{x}^{\mathrm{2}{n}} −\mathrm{1}}{{x}^{\mathrm{2}{n}+\mathrm{2}} }\:+\mathrm{2}{n}\:\:\:\:\left({x}\neq\overset{−} {+}\mathrm{1}\right) \\ $$$${n}=\mathrm{10}\:\Rightarrow\:{A}_{\mathrm{10}} \left({x}\right)\:\:=\frac{{x}^{\mathrm{2}} −{x}^{\mathrm{22}} }{\mathrm{1}−{x}^{\mathrm{2}} }\:+\frac{{x}^{\mathrm{20}} −\mathrm{1}}{{x}^{\mathrm{22}} }\:+\mathrm{20} \\ $$
Answered by TANMAY PANACEA. last updated on 25/Mar/20
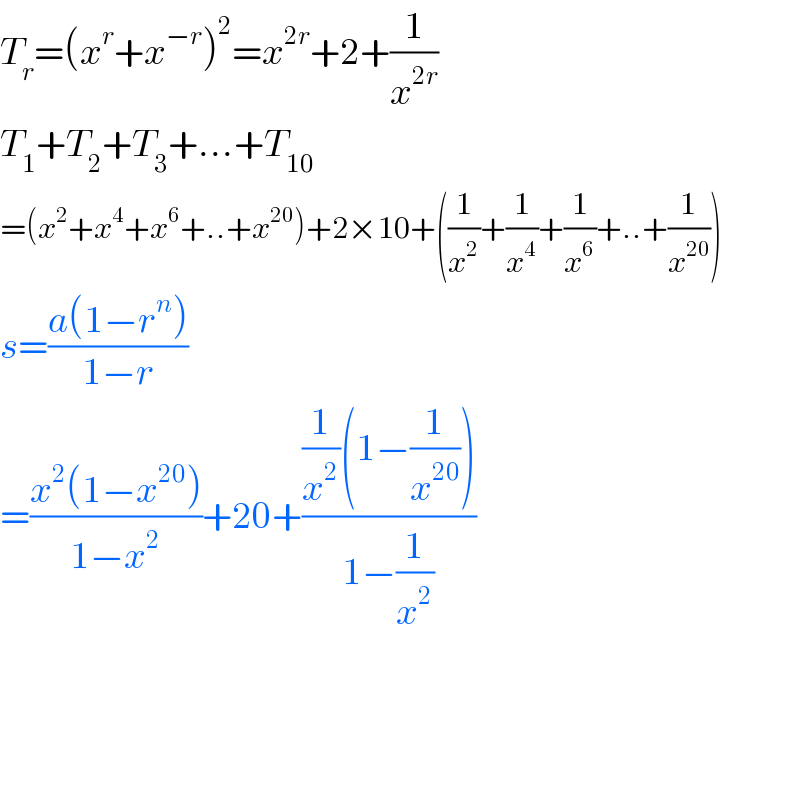
$${T}_{{r}} =\left({x}^{{r}} +{x}^{−{r}} \right)^{\mathrm{2}} ={x}^{\mathrm{2}{r}} +\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}{r}} } \\ $$$${T}_{\mathrm{1}} +{T}_{\mathrm{2}} +{T}_{\mathrm{3}} +…+{T}_{\mathrm{10}} \\ $$$$=\left({x}^{\mathrm{2}} +{x}^{\mathrm{4}} +{x}^{\mathrm{6}} +..+{x}^{\mathrm{20}} \right)+\mathrm{2}×\mathrm{10}+\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{{x}^{\mathrm{6}} }+..+\frac{\mathrm{1}}{{x}^{\mathrm{20}} }\right) \\ $$$${s}=\frac{{a}\left(\mathrm{1}−{r}^{{n}} \right)}{\mathrm{1}−{r}} \\ $$$$=\frac{{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{20}} \right)}{\mathrm{1}−{x}^{\mathrm{2}} }+\mathrm{20}+\frac{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{20}} }\right)}{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by jagoll last updated on 25/Mar/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
