Question Number 129377 by pipin last updated on 15/Jan/21

$$\int\frac{\:\sqrt{\boldsymbol{\mathrm{x}}}}{\:\sqrt{\boldsymbol{\mathrm{x}}-\mathrm{1}}}\mathrm{dx}\:=\:… \\ $$
Answered by Ar Brandon last updated on 15/Jan/21
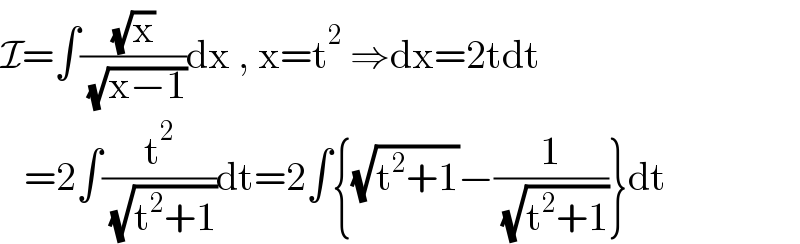
$$\mathcal{I}=\int\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{x}−\mathrm{1}}}\mathrm{dx}\:,\:\mathrm{x}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{dx}=\mathrm{2tdt} \\ $$$$\:\:\:=\mathrm{2}\int\frac{\mathrm{t}^{\mathrm{2}} }{\:\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}}\mathrm{dt}=\mathrm{2}\int\left\{\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}}\right\}\mathrm{dt} \\ $$
Answered by liberty last updated on 15/Jan/21
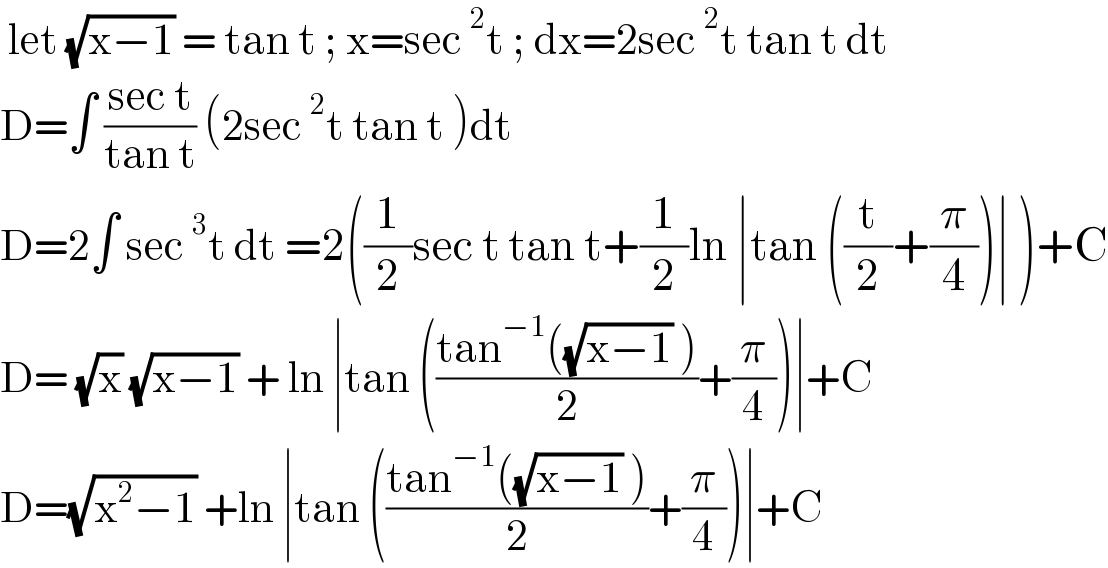
$$\:\mathrm{let}\:\sqrt{\mathrm{x}−\mathrm{1}}\:=\:\mathrm{tan}\:\mathrm{t}\:;\:\mathrm{x}=\mathrm{sec}\:^{\mathrm{2}} \mathrm{t}\:;\:\mathrm{dx}=\mathrm{2sec}\:^{\mathrm{2}} \mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:\mathrm{dt} \\ $$$$\mathrm{D}=\int\:\frac{\mathrm{sec}\:\mathrm{t}}{\mathrm{tan}\:\mathrm{t}}\:\left(\mathrm{2sec}\:^{\mathrm{2}} \mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:\right)\mathrm{dt}\:\: \\ $$$$\mathrm{D}=\mathrm{2}\int\:\mathrm{sec}\:^{\mathrm{3}} \mathrm{t}\:\mathrm{dt}\:=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{tan}\:\left(\frac{\mathrm{t}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\mid\:\right)+\mathrm{C} \\ $$$$\mathrm{D}=\:\sqrt{\mathrm{x}}\:\sqrt{\mathrm{x}−\mathrm{1}}\:+\:\mathrm{ln}\:\mid\mathrm{tan}\:\left(\frac{\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}−\mathrm{1}}\:\right)}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\mid+\mathrm{C} \\ $$$$\mathrm{D}=\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:+\mathrm{ln}\:\mid\mathrm{tan}\:\left(\frac{\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}−\mathrm{1}}\:\right)}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\mid+\mathrm{C} \\ $$
