Question Number 96596 by bemath last updated on 03/Jun/20
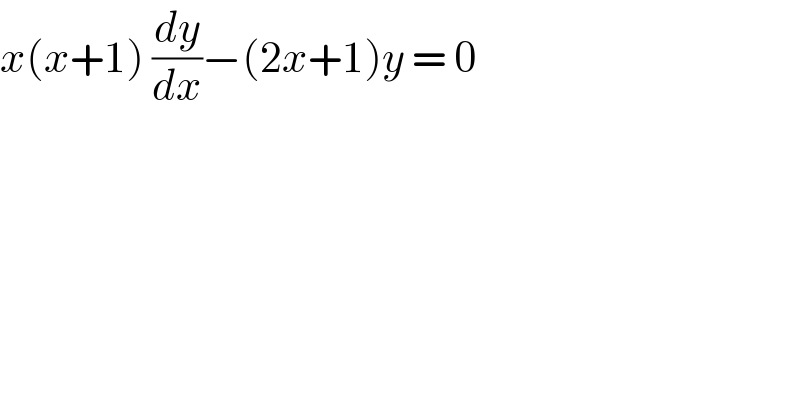
$${x}\left({x}+\mathrm{1}\right)\:\frac{{dy}}{{dx}}−\left(\mathrm{2}{x}+\mathrm{1}\right){y}\:=\:\mathrm{0} \\ $$
Answered by bobhans last updated on 03/Jun/20
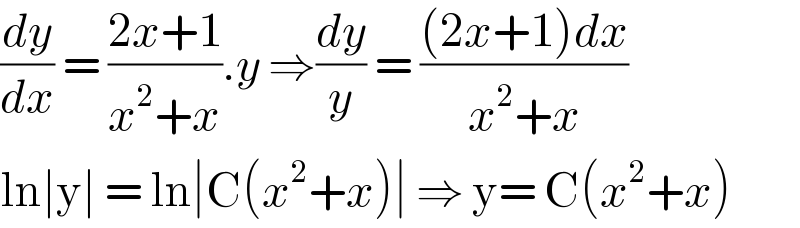
$$\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}}.{y}\:\Rightarrow\frac{{dy}}{{y}}\:=\:\frac{\left(\mathrm{2}{x}+\mathrm{1}\right){dx}}{{x}^{\mathrm{2}} +{x}} \\ $$$$\mathrm{ln}\mid\mathrm{y}\mid\:=\:\mathrm{ln}\mid\mathrm{C}\left({x}^{\mathrm{2}} +{x}\right)\mid\:\Rightarrow\:\mathrm{y}=\:\mathrm{C}\left({x}^{\mathrm{2}} +{x}\right) \\ $$
Answered by mathmax by abdo last updated on 03/Jun/20
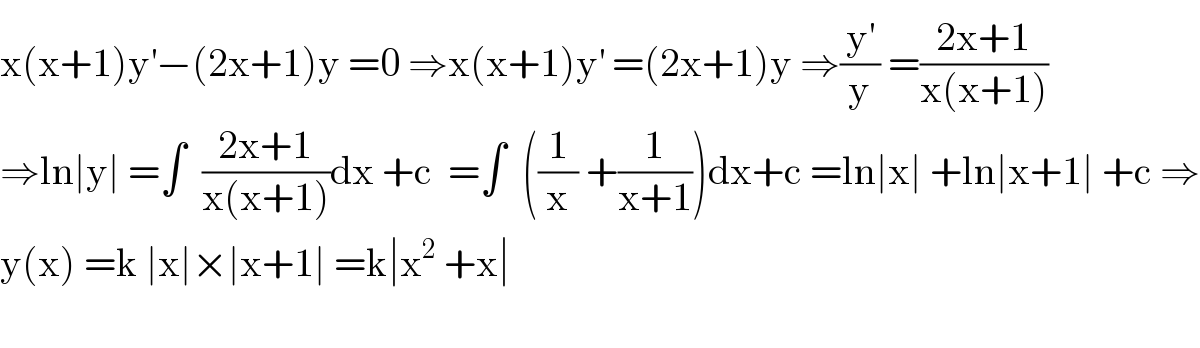
$$\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\mathrm{y}^{'} −\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{y}\:=\mathrm{0}\:\Rightarrow\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\mathrm{y}^{'} \:=\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{y}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)} \\ $$$$\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=\int\:\:\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{dx}\:+\mathrm{c}\:\:=\int\:\:\left(\frac{\mathrm{1}}{\mathrm{x}}\:+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)\mathrm{dx}+\mathrm{c}\:=\mathrm{ln}\mid\mathrm{x}\mid\:+\mathrm{ln}\mid\mathrm{x}+\mathrm{1}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{k}\:\mid\mathrm{x}\mid×\mid\mathrm{x}+\mathrm{1}\mid\:=\mathrm{k}\mid\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}\mid \\ $$$$ \\ $$
