x-x-2-1-x-x-2-1-x-x-2-1-x-x-2-1-98-

Question Number 114668 by bemath last updated on 20/Sep/20

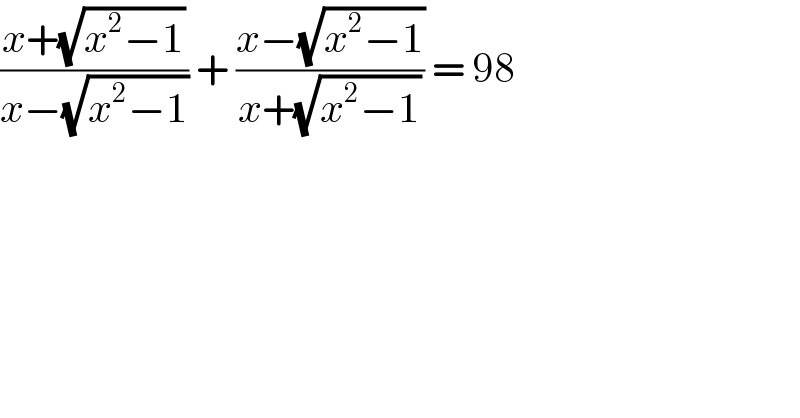
$$\frac{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:+\:\frac{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\:\mathrm{98}\: \\ $$

Answered by som(math1967) last updated on 20/Sep/20

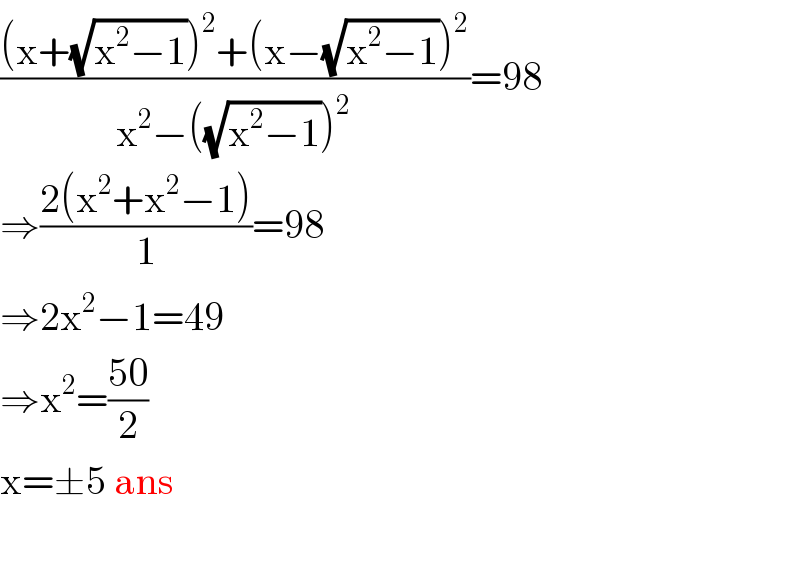
(((x+(√(x^2 −1)))^2 +(x−(√(x^2 −1)))^2 )/(x^2 −((√(x^2 −1)))^2 ))=98 ⇒((2(x^2 +x^2 −1))/1)=98 ⇒2x^2 −1=49 ⇒x^2 =((50)/2) x=±5 ans

$$\frac{\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} +\left(\mathrm{x}−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} −\left(\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} }=\mathrm{98} \\ $$$$\Rightarrow\frac{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{1}}=\mathrm{98} \\ $$$$\Rightarrow\mathrm{2x}^{\mathrm{2}} −\mathrm{1}=\mathrm{49} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{50}}{\mathrm{2}} \\ $$$$\mathrm{x}=\pm\mathrm{5}\:\mathrm{ans} \\ $$$$ \\ $$

Commented by bemath last updated on 20/Sep/20