x-x-2-2048-x-

Question Number 161951 by mathlove last updated on 24/Dec/21

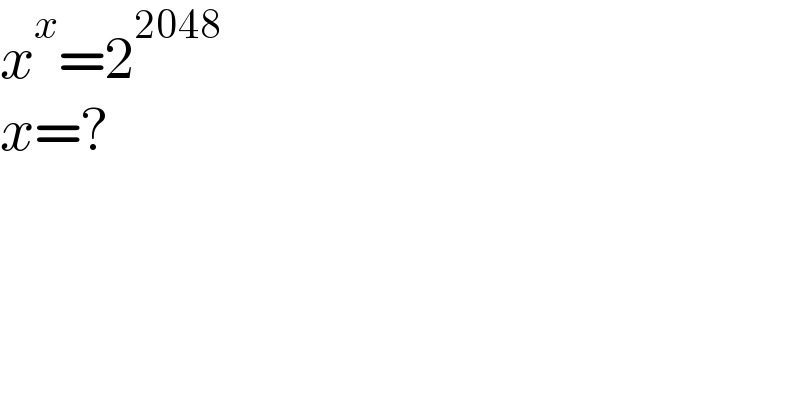
$${x}^{{x}} =\mathrm{2}^{\mathrm{2048}} \\ $$$${x}=? \\ $$

Answered by aleks041103 last updated on 24/Dec/21

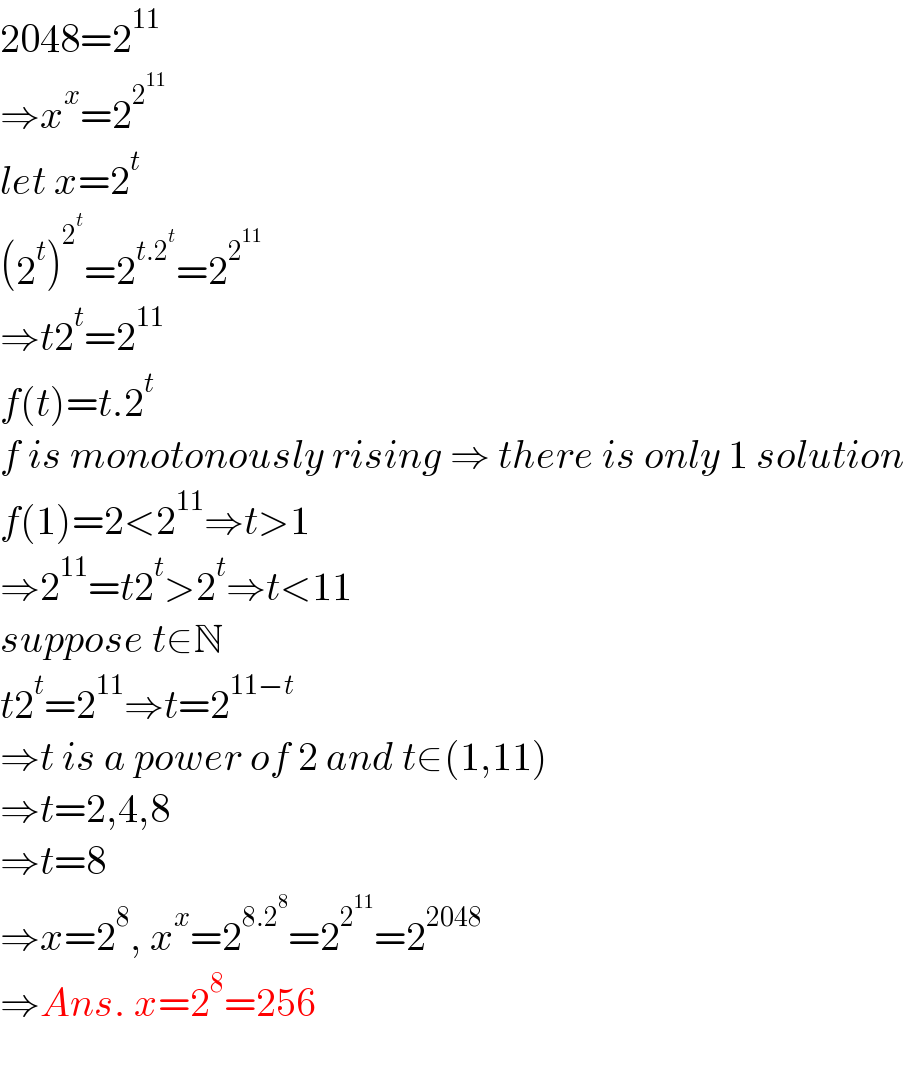
2048=2^(11) ⇒x^x =2^2^(11) let x=2^t (2^t )^2^t =2^(t.2^t ) =2^2^(11) ⇒t2^t =2^(11) f(t)=t.2^t f is monotonously rising ⇒ there is only 1 solution f(1)=2<2^(11) ⇒t>1 ⇒2^(11) =t2^t >2^t ⇒t<11 suppose t∈N t2^t =2^(11) ⇒t=2^(11−t) ⇒t is a power of 2 and t∈(1,11) ⇒t=2,4,8 ⇒t=8 ⇒x=2^8 , x^x =2^(8.2^8 ) =2^2^(11) =2^(2048) ⇒Ans. x=2^8 =256

$$\mathrm{2048}=\mathrm{2}^{\mathrm{11}} \\ $$$$\Rightarrow{x}^{{x}} =\mathrm{2}^{\mathrm{2}^{\mathrm{11}} } \\ $$$${let}\:{x}=\mathrm{2}^{{t}} \\ $$$$\left(\mathrm{2}^{{t}} \right)^{\mathrm{2}^{{t}} } =\mathrm{2}^{{t}.\mathrm{2}^{{t}} } =\mathrm{2}^{\mathrm{2}^{\mathrm{11}} } \\ $$$$\Rightarrow{t}\mathrm{2}^{{t}} =\mathrm{2}^{\mathrm{11}} \\ $$$${f}\left({t}\right)={t}.\mathrm{2}^{{t}} \\ $$$${f}\:{is}\:{monotonously}\:{rising}\:\Rightarrow\:{there}\:{is}\:{only}\:\mathrm{1}\:{solution} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{2}<\mathrm{2}^{\mathrm{11}} \Rightarrow{t}>\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{11}} ={t}\mathrm{2}^{{t}} >\mathrm{2}^{{t}} \Rightarrow{t}<\mathrm{11} \\ $$$${suppose}\:{t}\in\mathbb{N}\:\: \\ $$$${t}\mathrm{2}^{{t}} =\mathrm{2}^{\mathrm{11}} \Rightarrow{t}=\mathrm{2}^{\mathrm{11}−{t}} \\ $$$$\Rightarrow{t}\:{is}\:{a}\:{power}\:{of}\:\mathrm{2}\:{and}\:{t}\in\left(\mathrm{1},\mathrm{11}\right) \\ $$$$\Rightarrow{t}=\mathrm{2},\mathrm{4},\mathrm{8} \\ $$$$\Rightarrow{t}=\mathrm{8} \\ $$$$\Rightarrow{x}=\mathrm{2}^{\mathrm{8}} ,\:{x}^{{x}} =\mathrm{2}^{\mathrm{8}.\mathrm{2}^{\mathrm{8}} } =\mathrm{2}^{\mathrm{2}^{\mathrm{11}} } =\mathrm{2}^{\mathrm{2048}} \\ $$$$\Rightarrow{Ans}.\:{x}=\mathrm{2}^{\mathrm{8}} =\mathrm{256} \\ $$$$ \\ $$

Answered by mr W last updated on 24/Dec/21

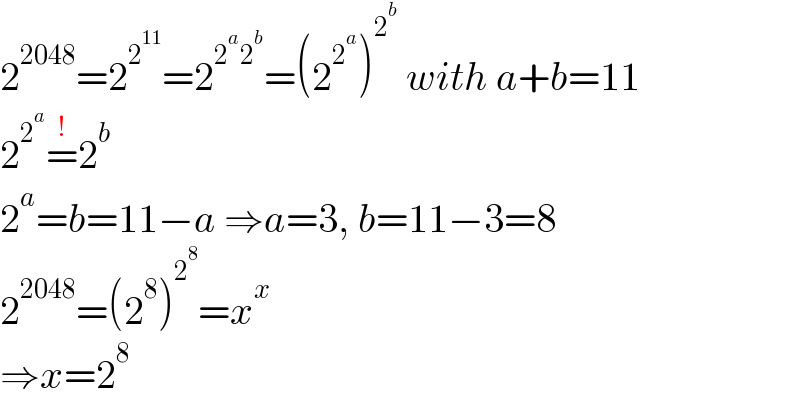
2^(2048) =2^2^(11) =2^(2^a 2^b ) =(2^2^a )^2^b with a+b=11 2^2^a =^(!) 2^b 2^a =b=11−a ⇒a=3, b=11−3=8 2^(2048) =(2^8 )^2^8 =x^x ⇒x=2^8

$$\mathrm{2}^{\mathrm{2048}} =\mathrm{2}^{\mathrm{2}^{\mathrm{11}} } =\mathrm{2}^{\mathrm{2}^{{a}} \mathrm{2}^{{b}} } =\left(\mathrm{2}^{\mathrm{2}^{{a}} } \right)^{\mathrm{2}^{{b}} } \:{with}\:{a}+{b}=\mathrm{11} \\ $$$$\mathrm{2}^{\mathrm{2}^{{a}} } \overset{!} {=}\mathrm{2}^{{b}} \\ $$$$\mathrm{2}^{{a}} ={b}=\mathrm{11}−{a}\:\Rightarrow{a}=\mathrm{3},\:{b}=\mathrm{11}−\mathrm{3}=\mathrm{8} \\ $$$$\mathrm{2}^{\mathrm{2048}} =\left(\mathrm{2}^{\mathrm{8}} \right)^{\mathrm{2}^{\mathrm{8}} } ={x}^{{x}} \\ $$$$\Rightarrow{x}=\mathrm{2}^{\mathrm{8}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply