Question Number 183806 by cortano1 last updated on 30/Dec/22
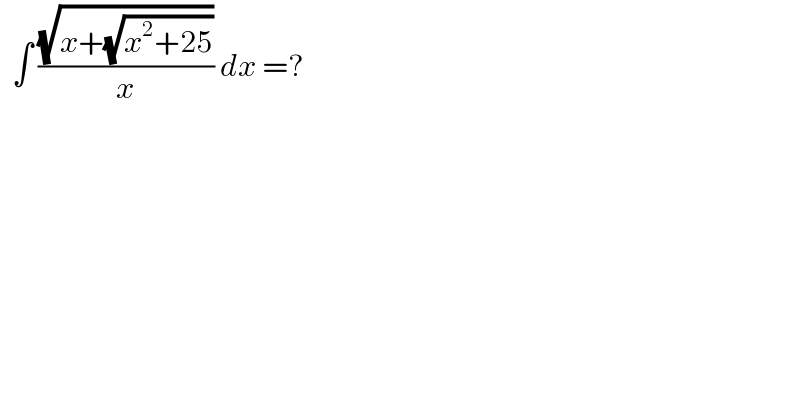
$$\:\:\int\:\frac{\sqrt{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{25}}}}{{x}}\:{dx}\:=? \\ $$
Answered by Ar Brandon last updated on 30/Dec/22

$${I}=\int\frac{\sqrt{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{25}}}}{{x}}{dx}\:,\:{x}=\mathrm{5sh}\vartheta \\ $$$$\:\:=\int\frac{\sqrt{\mathrm{5sh}\vartheta+\mathrm{5ch}\vartheta}}{\mathrm{5sh}\vartheta}\left(\mathrm{5ch}\vartheta{d}\vartheta\right)=\sqrt{\mathrm{5}}\int\left(\frac{{e}^{\mathrm{2}\vartheta} +\mathrm{1}}{{e}^{\mathrm{2}\vartheta} −\mathrm{1}}\right){e}^{\frac{\vartheta}{\mathrm{2}}} {d}\vartheta,\:\vartheta=\mathrm{2}\phi \\ $$$$\:\:=\mathrm{2}\sqrt{\mathrm{5}}\int\left(\frac{{e}^{\mathrm{4}\phi} +\mathrm{1}}{{e}^{\mathrm{4}\phi} −\mathrm{1}}\right){e}^{\phi} {d}\phi=\mathrm{2}\sqrt{\mathrm{5}}\int\left(\frac{{t}^{\mathrm{4}} +\mathrm{1}}{{t}^{\mathrm{4}} −\mathrm{1}}\right){dt}=\mathrm{2}\sqrt{\mathrm{5}}\int\left(\mathrm{1}+\frac{\mathrm{2}}{{t}^{\mathrm{4}} −\mathrm{1}}\right){dt},\:{t}={e}^{\phi} \\ $$$$\:\:=\mathrm{2}\sqrt{\mathrm{5}}\int\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt}=\mathrm{2}\sqrt{\mathrm{5}}\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid−\mathrm{arctan}\left({t}\right)\right)+{C} \\ $$$$\:\:=\mathrm{2}\sqrt{\mathrm{5}}\left({e}^{\frac{\vartheta}{\mathrm{2}}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid{e}^{\frac{\vartheta}{\mathrm{2}}} −\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid{e}^{\frac{\vartheta}{\mathrm{2}}} +\mathrm{1}\mid−\mathrm{arctan}\left({e}^{\frac{\vartheta}{\mathrm{2}}} \right)\right)+{C} \\ $$$$\:\:=\mathrm{2}\sqrt{\mathrm{5}}\sqrt{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{25}}}+\sqrt{\mathrm{5}}\mathrm{ln}\mid\frac{\sqrt{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{25}}}−\mathrm{1}}{\:\sqrt{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{25}}}+\mathrm{1}}\mid−\mathrm{2}\sqrt{\mathrm{5}}\mathrm{arctan}\left(\sqrt{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{25}}}\right)+{C} \\ $$
