Question Number 56991 by Tawa1 last updated on 28/Mar/19
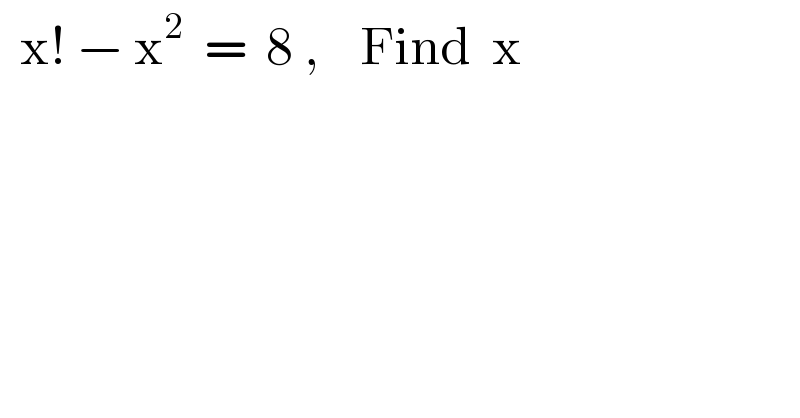
$$\:\:\mathrm{x}!\:−\:\mathrm{x}^{\mathrm{2}} \:\:=\:\:\mathrm{8}\:,\:\:\:\:\mathrm{Find}\:\:\mathrm{x} \\ $$$$ \\ $$
Commented by Joel578 last updated on 28/Mar/19

$${x}\:=\:\mathrm{4} \\ $$
Commented by Tawa1 last updated on 28/Mar/19
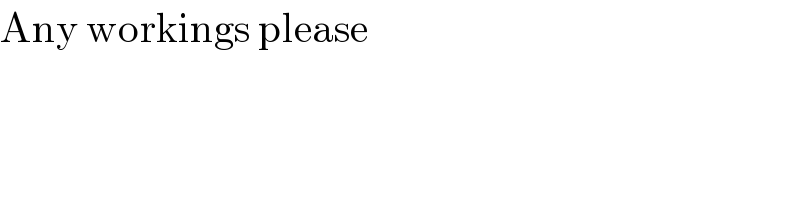
$$\mathrm{Any}\:\mathrm{workings}\:\mathrm{please} \\ $$
Commented by MJS last updated on 28/Mar/19
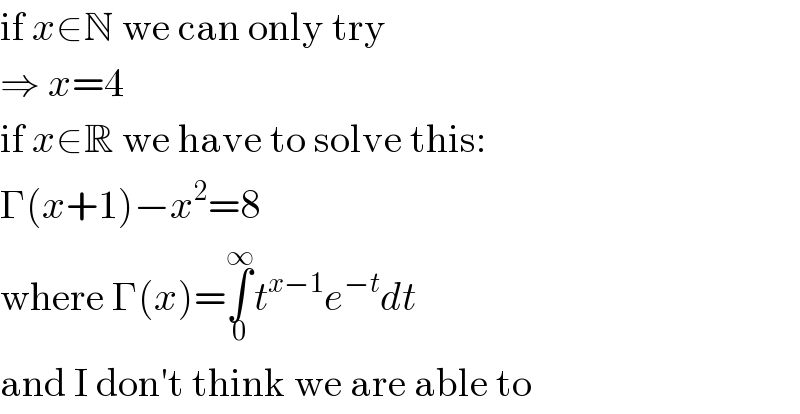
$$\mathrm{if}\:{x}\in\mathbb{N}\:\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{try} \\ $$$$\Rightarrow\:{x}=\mathrm{4} \\ $$$$\mathrm{if}\:{x}\in\mathbb{R}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}: \\ $$$$\Gamma\left({x}+\mathrm{1}\right)−{x}^{\mathrm{2}} =\mathrm{8} \\ $$$$\mathrm{where}\:\Gamma\left({x}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}{t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$\mathrm{and}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{are}\:\mathrm{able}\:\mathrm{to} \\ $$
Commented by maxmathsup by imad last updated on 28/Mar/19

$${sir}\:{tawa}\mathrm{1}\:{you}\:{must}\:{first}\:{define}\:{x}! \\ $$
