Question Number 101178 by bemath last updated on 01/Jul/20
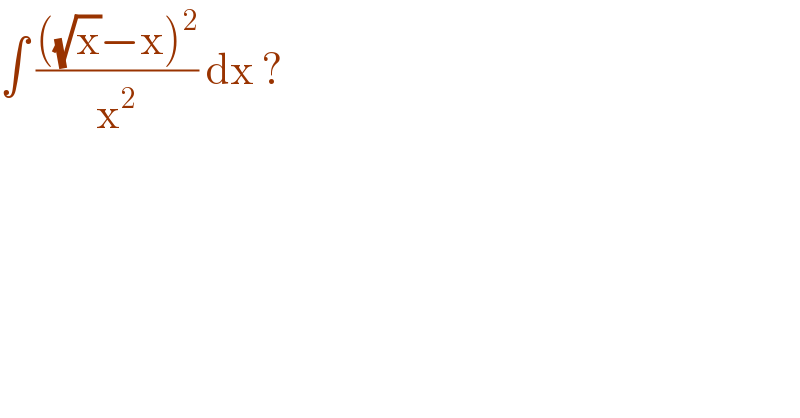
$$\int\:\frac{\left(\sqrt{\mathrm{x}}−\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:? \\ $$
Answered by bobhans last updated on 01/Jul/20

$$\int\:\frac{{x}−\mathrm{2}{x}^{\frac{\mathrm{3}}{\mathrm{2}}} +{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:{dx}\:=\:\int\frac{\mathrm{1}}{{x}}−\frac{\mathrm{2}}{\:\sqrt{{x}}}\:+\mathrm{1}\:{dx} \\ $$$$=\:\mathrm{ln}\mid{x}\mid\:−\:\mathrm{4}\sqrt{{x}}\:+\:{x}\:+\:{C} \\ $$$$\mathrm{it}\:\mathrm{easy}..= \\ $$
Answered by mathmax by abdo last updated on 01/Jul/20
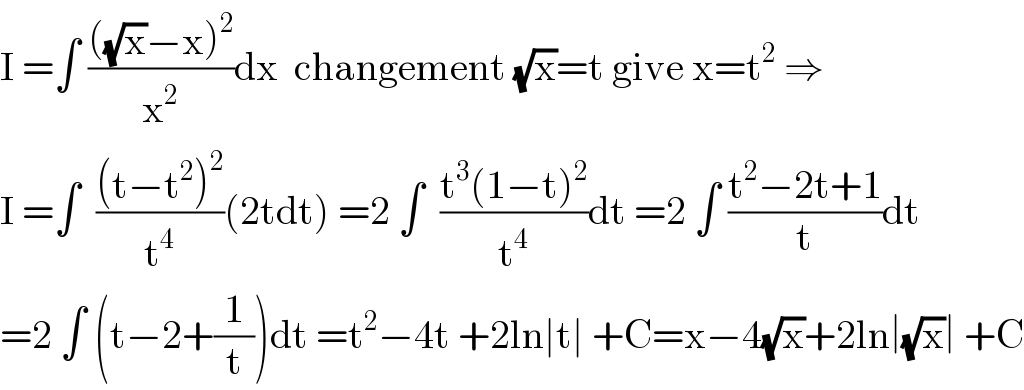
$$\mathrm{I}\:=\int\:\frac{\left(\sqrt{\mathrm{x}}−\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{changement}\:\sqrt{\mathrm{x}}=\mathrm{t}\:\mathrm{give}\:\mathrm{x}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\frac{\left(\mathrm{t}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{t}^{\mathrm{4}} }\left(\mathrm{2tdt}\right)\:=\mathrm{2}\:\int\:\:\frac{\mathrm{t}^{\mathrm{3}} \left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }{\mathrm{t}^{\mathrm{4}} }\mathrm{dt}\:=\mathrm{2}\:\int\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{2t}+\mathrm{1}}{\mathrm{t}}\mathrm{dt} \\ $$$$=\mathrm{2}\:\int\:\left(\mathrm{t}−\mathrm{2}+\frac{\mathrm{1}}{\mathrm{t}}\right)\mathrm{dt}\:=\mathrm{t}^{\mathrm{2}} −\mathrm{4t}\:+\mathrm{2ln}\mid\mathrm{t}\mid\:+\mathrm{C}=\mathrm{x}−\mathrm{4}\sqrt{\mathrm{x}}+\mathrm{2ln}\mid\sqrt{\mathrm{x}}\mid\:+\mathrm{C} \\ $$
