Question Number 124134 by bramlexs22 last updated on 01/Dec/20

$$\:\varphi\left({x}\right)=\:\int\:\left(\frac{{x}^{\mathrm{3}} +\mathrm{2}}{{x}^{\mathrm{3}} }\right)\:\sqrt{{x}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:{dx}\: \\ $$
Answered by Dwaipayan Shikari last updated on 01/Dec/20
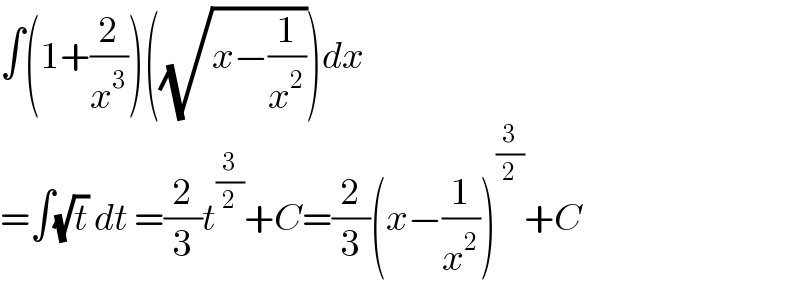
$$\int\left(\mathrm{1}+\frac{\mathrm{2}}{{x}^{\mathrm{3}} }\right)\left(\sqrt{{x}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\right){dx} \\ $$$$=\int\sqrt{{t}}\:{dt}\:=\frac{\mathrm{2}}{\mathrm{3}}{t}^{\frac{\mathrm{3}}{\mathrm{2}}} +{C}=\frac{\mathrm{2}}{\mathrm{3}}\left({x}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{C} \\ $$
