x-x-3-x-faind-x-

Question Number 185599 by mathlove last updated on 24/Jan/23

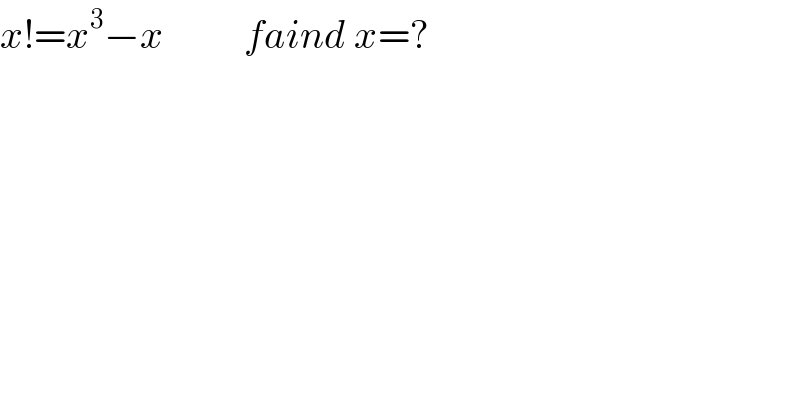
$${x}!={x}^{\mathrm{3}} −{x}\:\:\:\:\:\:\:\:\:\:{faind}\:{x}=? \\ $$

Commented by liuxinnan last updated on 24/Jan/23

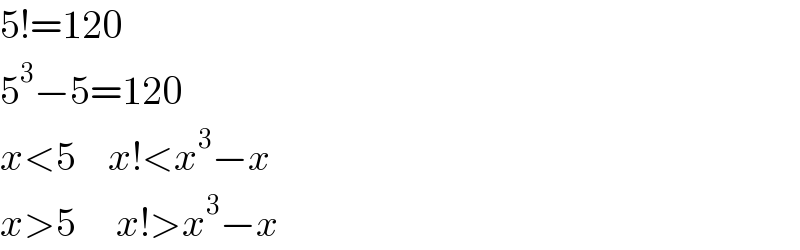
5!=120 5^3 −5=120 x<5 x!<x^3 −x x>5 x!>x^3 −x

$$\mathrm{5}!=\mathrm{120} \\ $$$$\mathrm{5}^{\mathrm{3}} −\mathrm{5}=\mathrm{120} \\ $$$${x}<\mathrm{5}\:\:\:\:{x}!<{x}^{\mathrm{3}} −{x} \\ $$$${x}>\mathrm{5}\:\:\:\:\:{x}!>{x}^{\mathrm{3}} −{x} \\ $$

Commented by Rasheed.Sindhi last updated on 24/Jan/23

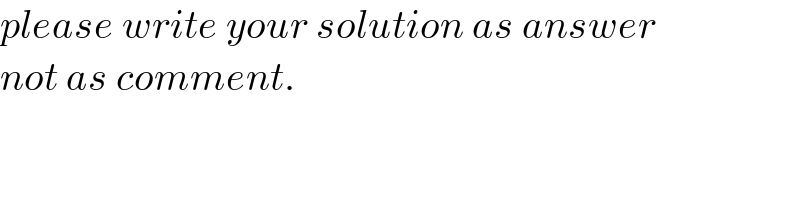
$${please}\:{write}\:{your}\:{solution}\:{as}\:{answer} \\ $$$${not}\:{as}\:{comment}. \\ $$

Commented by liuxinnan last updated on 24/Jan/23

$${next}\:{must} \\ $$

Answered by Frix last updated on 24/Jan/23

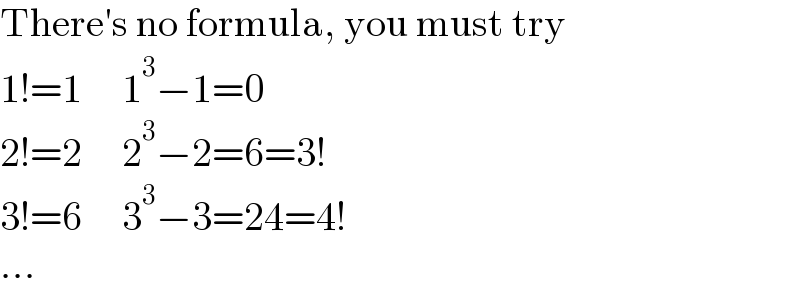
There′s no formula, you must try 1!=1 1^3 −1=0 2!=2 2^3 −2=6=3! 3!=6 3^3 −3=24=4! ...

$$\mathrm{There}'\mathrm{s}\:\mathrm{no}\:\mathrm{formula},\:\mathrm{you}\:\mathrm{must}\:\mathrm{try} \\ $$$$\mathrm{1}!=\mathrm{1}\:\:\:\:\:\mathrm{1}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{2}!=\mathrm{2}\:\:\:\:\:\mathrm{2}^{\mathrm{3}} −\mathrm{2}=\mathrm{6}=\mathrm{3}! \\ $$$$\mathrm{3}!=\mathrm{6}\:\:\:\:\:\mathrm{3}^{\mathrm{3}} −\mathrm{3}=\mathrm{24}=\mathrm{4}! \\ $$$$… \\ $$

Answered by ajfour last updated on 24/Jan/23

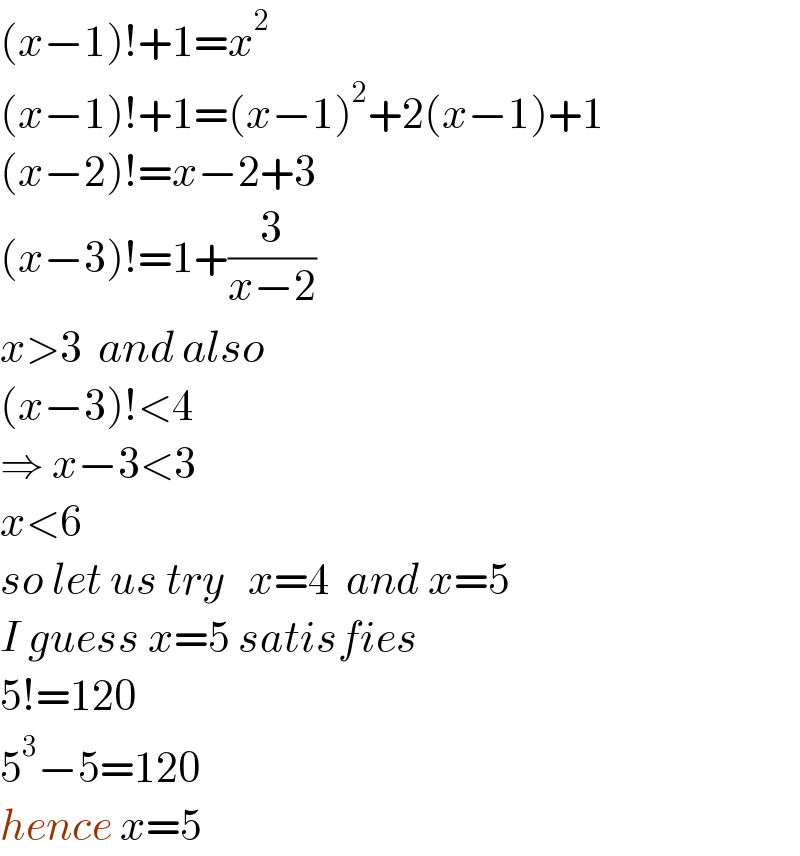
(x−1)!+1=x^2 (x−1)!+1=(x−1)^2 +2(x−1)+1 (x−2)!=x−2+3 (x−3)!=1+(3/(x−2)) x>3 and also (x−3)!<4 ⇒ x−3<3 x<6 so let us try x=4 and x=5 I guess x=5 satisfies 5!=120 5^3 −5=120 hence x=5

$$\left({x}−\mathrm{1}\right)!+\mathrm{1}={x}^{\mathrm{2}} \\ $$$$\left({x}−\mathrm{1}\right)!+\mathrm{1}=\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$$\left({x}−\mathrm{2}\right)!={x}−\mathrm{2}+\mathrm{3} \\ $$$$\left({x}−\mathrm{3}\right)!=\mathrm{1}+\frac{\mathrm{3}}{{x}−\mathrm{2}} \\ $$$${x}>\mathrm{3}\:\:{and}\:{also} \\ $$$$\left({x}−\mathrm{3}\right)!<\mathrm{4} \\ $$$$\Rightarrow\:{x}−\mathrm{3}<\mathrm{3} \\ $$$${x}<\mathrm{6} \\ $$$${so}\:{let}\:{us}\:{try}\:\:\:{x}=\mathrm{4}\:\:{and}\:{x}=\mathrm{5} \\ $$$${I}\:{guess}\:{x}=\mathrm{5}\:{satisfies} \\ $$$$\mathrm{5}!=\mathrm{120} \\ $$$$\mathrm{5}^{\mathrm{3}} −\mathrm{5}=\mathrm{120} \\ $$$${hence}\:{x}=\mathrm{5} \\ $$

Commented by mathlove last updated on 24/Jan/23

$${thanks} \\ $$

Answered by Rasheed.Sindhi last updated on 24/Jan/23

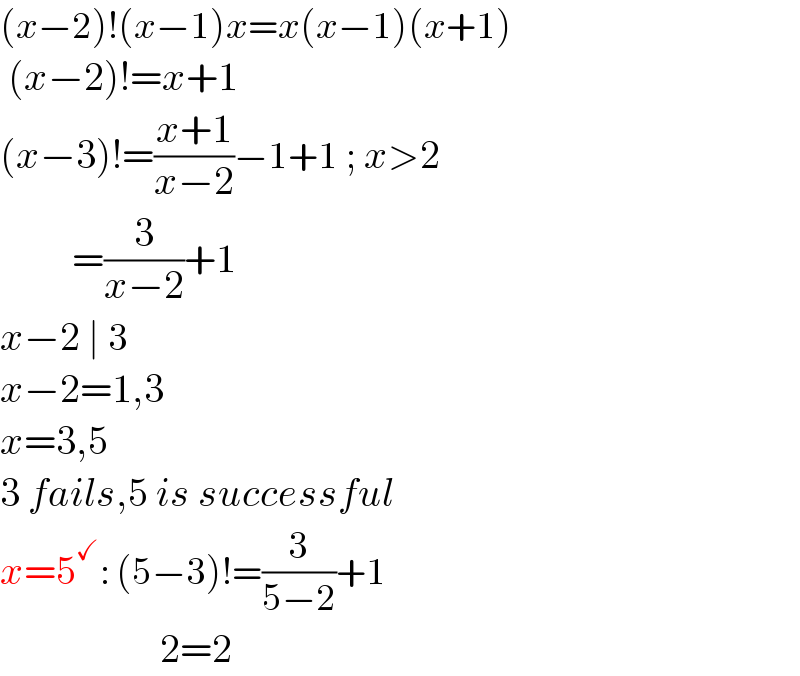
(x−2)!(x−1)x=x(x−1)(x+1) (x−2)!=x+1 (x−3)!=((x+1)/(x−2))−1+1 ; x>2 =(3/(x−2))+1 x−2 ∣ 3 x−2=1,3 x=3,5 3 fails,5 is successful x=5^✓ : (5−3)!=(3/(5−2))+1 2=2

$$\left({x}−\mathrm{2}\right)!\left({x}−\mathrm{1}\right){x}={x}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right) \\ $$$$\:\left({x}−\mathrm{2}\right)!={x}+\mathrm{1} \\ $$$$\left({x}−\mathrm{3}\right)!=\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}−\mathrm{1}+\mathrm{1}\:;\:{x}>\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}}{{x}−\mathrm{2}}+\mathrm{1} \\ $$$${x}−\mathrm{2}\:\mid\:\mathrm{3} \\ $$$${x}−\mathrm{2}=\mathrm{1},\mathrm{3} \\ $$$${x}=\mathrm{3},\mathrm{5} \\ $$$$\mathrm{3}\:{fails},\mathrm{5}\:{is}\:{successful} \\ $$$${x}=\mathrm{5}^{\checkmark} :\:\left(\mathrm{5}−\mathrm{3}\right)!=\frac{\mathrm{3}}{\mathrm{5}−\mathrm{2}}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}=\mathrm{2} \\ $$

Answered by SEKRET last updated on 24/Jan/23

x∙(x−1)∙(x−2)!=x∙(x−1)(x+1) (x−2)!=x−2+3 a!=a+3 a>0 1=4 2=5 6=6 a=3 24=7 >> x−2=3 x=5 ✅

$$\:\boldsymbol{\mathrm{x}}\centerdot\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\centerdot\left(\boldsymbol{\mathrm{x}}−\mathrm{2}\right)!=\boldsymbol{\mathrm{x}}\centerdot\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\left(\boldsymbol{\mathrm{x}}+\mathrm{1}\right) \\ $$$$\:\:\:\left(\boldsymbol{\mathrm{x}}−\mathrm{2}\right)!=\boldsymbol{\mathrm{x}}−\mathrm{2}+\mathrm{3} \\ $$$$\:\:\:\boldsymbol{\mathrm{a}}!=\boldsymbol{\mathrm{a}}+\mathrm{3}\:\:\:\:\boldsymbol{\mathrm{a}}>\mathrm{0} \\ $$$$\:\:\:\mathrm{1}=\mathrm{4} \\ $$$$\:\:\:\:\mathrm{2}=\mathrm{5} \\ $$$$\:\:\:\:\mathrm{6}=\mathrm{6}\:\:\:\:\:\boldsymbol{\mathrm{a}}=\mathrm{3} \\ $$$$\:\mathrm{24}=\mathrm{7}\:\:>> \\ $$$$\:\:\boldsymbol{\mathrm{x}}−\mathrm{2}=\mathrm{3} \\ $$$$\:\:\boldsymbol{\mathrm{x}}=\mathrm{5} \\ $$$$ \\ $$$$ \\ $$✅

Facebook Tweet Pin

Leave a Reply Cancel reply