Menu Close

x-x-4-x-2-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 36643 by rahul 19 last updated on 03/Jun/18
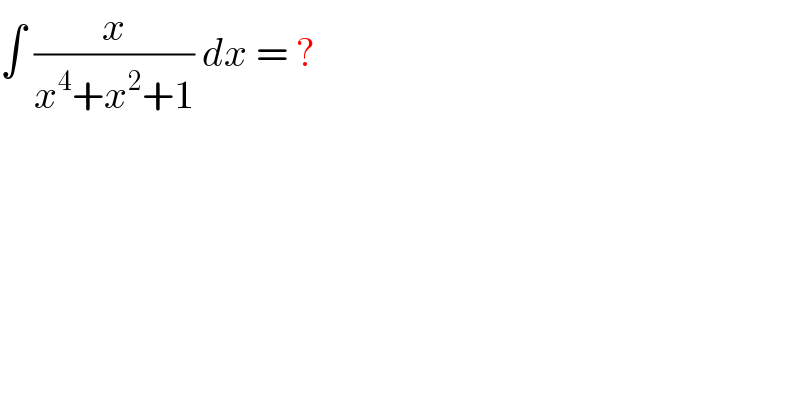
∫ (x/(x^4 +x^2 +1)) dx = ?
$$\int\:\frac{{x}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}\:=\:? \\ $$
Commented by math khazana by abdo last updated on 09/Aug/18
changement x^2 =t give 2xdx=dt I = ∫ (1/(t^2 +t +1)) (dt/2) =(1/2) ∫ (dt/((t+(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) (1/2) (4/3) ∫ (1/(1+u^2 )) ((√3)/2) du =(1/( (√3))) arctanu +c=(1/( (√3))) arctan(((2t+1)/( (√3))))+c I =(1/( (√3))) arctan(((2x^2 +1)/( (√3)))) +c
$${changement}\:{x}^{\mathrm{2}} ={t}\:{give}\:\mathrm{2}{xdx}={dt} \\ $$$${I}\:\:=\:\int\:\:\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}\:\frac{{dt}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\:\:\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=_{{t}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{4}}{\mathrm{3}}\:\int\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{du} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{arctanu}\:+{c}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+{c} \\ $$$${I}\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+{c} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Jun/18
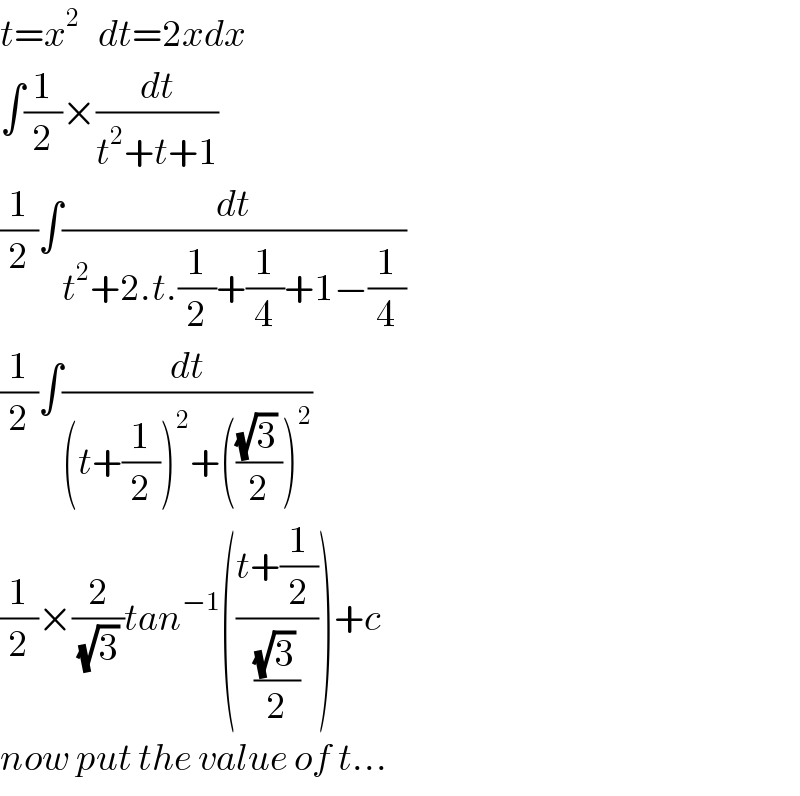
t=x^2 dt=2xdx ∫(1/2)×(dt/(t^2 +t+1)) (1/2)∫(dt/(t^2 +2.t.(1/2)+(1/4)+1−(1/4))) (1/2)∫(dt/((t+(1/2))^2 +((((√3) )/2))^2 )) (1/2)×(2/( (√3) ))tan^(−1) (((t+(1/2))/(((√3) )/2)))+c now put the value of t...
$${t}={x}^{\mathrm{2}} \:\:\:{dt}=\mathrm{2}{xdx} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{2}}×\frac{{dt}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}.{t}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}\:}{tan}^{−\mathrm{1}} \left(\frac{{t}+\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}}\right)+{c} \\ $$$${now}\:{put}\:{the}\:{value}\:{of}\:{t}… \\ $$
Commented by rahul 19 last updated on 03/Jun/18
thank you sir ����
Answered by MJS last updated on 03/Jun/18
∫(x/(x^4 +x^2 +1))dx= [t=x^2 → dx=(dt/(2x))] =(1/2)∫(dt/(t^2 +t+1))=(1/2)∫(dt/((t+(1/2))^2 +(3/4)))= [u=((√3)/3)(2t+1) → dt=((√3)/2)du] =((√3)/3)∫(du/(u^2 +1))=((√3)/3)arctan u=((√3)/3)arctan(((√3)/3)(2t+1))= =((√3)/3)arctan(((√3)/3)(2x^2 +1))+C
$$\int\frac{{x}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}={x}^{\mathrm{2}} \:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}{x}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)\:\rightarrow\:{dt}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{du}\right] \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:{u}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)\right)= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)\right)+{C} \\ $$
Commented by rahul 19 last updated on 03/Jun/18
thank you sir. ����

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *