x-x-64-x-

Question Number 148395 by mathdanisur last updated on 27/Jul/21

$$\boldsymbol{{x}}^{\boldsymbol{{x}}} \:=\:\mathrm{64} \\ $$$$\Rightarrow\:\boldsymbol{{x}}\:=\:? \\ $$

Answered by Math_Freak last updated on 27/Jul/21

if x>0 xlnx = ln64 xlnx = ln2^6 xlnx = 6ln2 (e^(lnx) )•lnx = 6ln2 introducing lambert function lnx = W(6ln2) x = e^(W(6ln2)) ≈ 3.39121540052283312 if x<0 let x = −u xlnx = 6ln2 −uln∣−u∣ = 6ln2 −ulnu = 6ln2 ulnu = −6ln2 (e^(lnu) )•lnu = −6ln2 introducing product log lnu = W(−6ln2) u = e^(W(−6ln2)) x = −u x = −e^(W(−6ln2)) ≈ 0.7007 − 1.9045 i

$${if}\:{x}>\mathrm{0} \\ $$$${xlnx}\:=\:{ln}\mathrm{64} \\ $$$${xlnx}\:=\:{ln}\mathrm{2}^{\mathrm{6}} \\ $$$${xlnx}\:=\:\mathrm{6}{ln}\mathrm{2} \\ $$$$\left({e}^{{lnx}} \right)\bullet{lnx}\:=\:\mathrm{6}{ln}\mathrm{2} \\ $$$${introducing}\:{lambert}\:{function} \\ $$$${lnx}\:=\:{W}\left(\mathrm{6}{ln}\mathrm{2}\right) \\ $$$${x}\:=\:{e}^{{W}\left(\mathrm{6}{ln}\mathrm{2}\right)} \:\approx\:\mathrm{3}.\mathrm{39121540052283312} \\ $$$$ \\ $$$${if}\:{x}<\mathrm{0} \\ $$$${let}\:{x}\:=\:−{u} \\ $$$${xlnx}\:=\:\mathrm{6}{ln}\mathrm{2} \\ $$$$−{uln}\mid−{u}\mid\:=\:\mathrm{6}{ln}\mathrm{2} \\ $$$$−{ulnu}\:=\:\mathrm{6}{ln}\mathrm{2} \\ $$$${ulnu}\:=\:−\mathrm{6}{ln}\mathrm{2} \\ $$$$\left({e}^{{lnu}} \right)\bullet{lnu}\:=\:−\mathrm{6}{ln}\mathrm{2} \\ $$$${introducing}\:{product}\:{log} \\ $$$${lnu}\:=\:{W}\left(−\mathrm{6}{ln}\mathrm{2}\right) \\ $$$${u}\:=\:{e}^{{W}\left(−\mathrm{6}{ln}\mathrm{2}\right)} \\ $$$${x}\:=\:−{u} \\ $$$${x}\:=\:−{e}^{{W}\left(−\mathrm{6}{ln}\mathrm{2}\right)} \:\approx\:\mathrm{0}.\mathrm{7007}\:−\:\mathrm{1}.\mathrm{9045}\:{i} \\ $$

Commented by Tawa11 last updated on 27/Jul/21

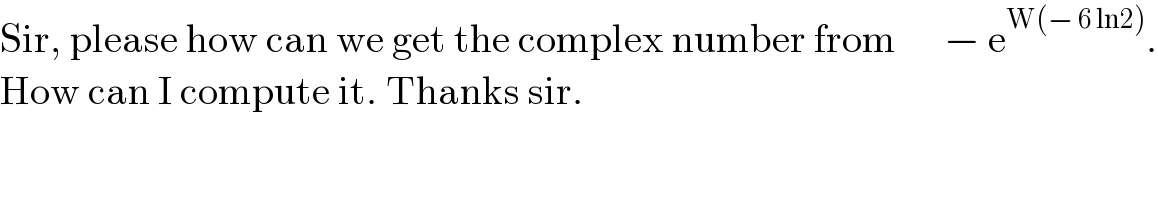
Sir, please how can we get the complex number from − e^(W(− 6 ln2)) . How can I compute it. Thanks sir.

$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{how}\:\mathrm{can}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{number}\:\mathrm{from}\:\:\:\:\:\:−\:\mathrm{e}^{\mathrm{W}\left(−\:\mathrm{6}\:\mathrm{ln2}\right)} . \\ $$$$\mathrm{How}\:\mathrm{can}\:\mathrm{I}\:\mathrm{compute}\:\mathrm{it}.\:\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Commented by Math_Freak last updated on 27/Jul/21

Use wolfram Alpha search for wolfram Alpha on the web to compute W(2ln2) type productlog(2ln2)

$${Use}\:{wolfram}\:{Alpha} \\ $$$${search}\:{for}\:{wolfram}\:{Alpha}\:{on}\:{the} \\ $$$${web} \\ $$$$ \\ $$$${to}\:{compute}\:{W}\left(\mathrm{2}{ln}\mathrm{2}\right) \\ $$$${type}\:{productlog}\left(\mathrm{2}{ln}\mathrm{2}\right) \\ $$

Commented by mathdanisur last updated on 27/Jul/21

$${Thankyou}\:{Sir}\:{cool} \\ $$

Commented by mathdanisur last updated on 27/Jul/21

$${Answer}\:{Sir}.? \\ $$

Commented by mr W last updated on 27/Jul/21

(0.7007 − 1.9045 i)^((0.7007 − 1.9045 i)) ≠64

$$\left(\mathrm{0}.\mathrm{7007}\:−\:\mathrm{1}.\mathrm{9045}\:{i}\right)^{\left(\mathrm{0}.\mathrm{7007}\:−\:\mathrm{1}.\mathrm{9045}\:{i}\right)} \neq\mathrm{64} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply