Question Number 96329 by M±th+et+s last updated on 31/May/20
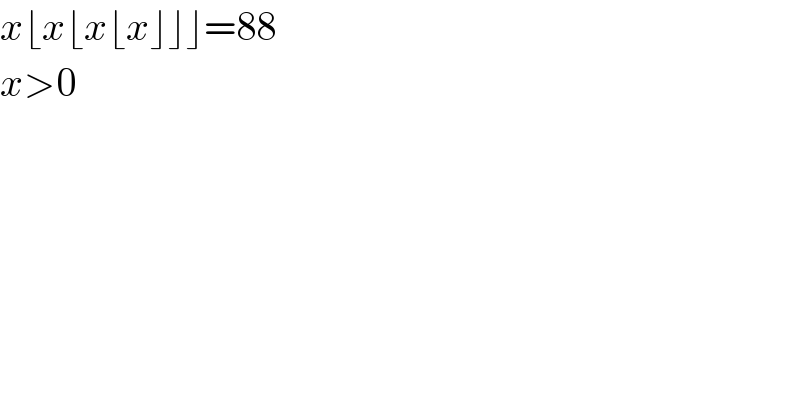
$${x}\lfloor{x}\lfloor{x}\lfloor{x}\rfloor\rfloor\rfloor=\mathrm{88} \\ $$$${x}>\mathrm{0} \\ $$
Commented by prakash jain last updated on 31/May/20
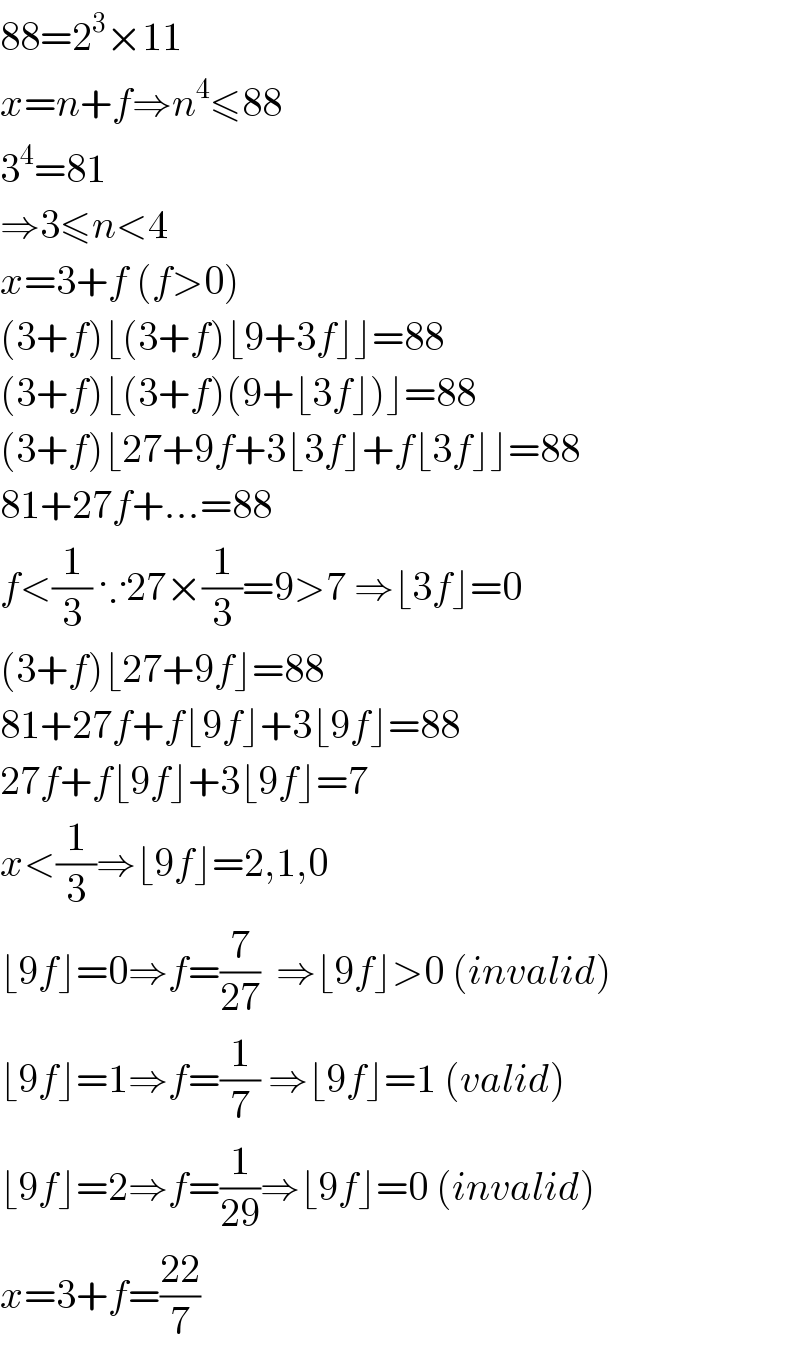
$$\mathrm{88}=\mathrm{2}^{\mathrm{3}} ×\mathrm{11} \\ $$$${x}={n}+{f}\Rightarrow{n}^{\mathrm{4}} \leqslant\mathrm{88} \\ $$$$\mathrm{3}^{\mathrm{4}} =\mathrm{81} \\ $$$$\Rightarrow\mathrm{3}\leqslant{n}<\mathrm{4} \\ $$$${x}=\mathrm{3}+{f}\:\left({f}>\mathrm{0}\right) \\ $$$$\left(\mathrm{3}+{f}\right)\lfloor\left(\mathrm{3}+{f}\right)\lfloor\mathrm{9}+\mathrm{3}{f}\rfloor\rfloor=\mathrm{88} \\ $$$$\left(\mathrm{3}+{f}\right)\lfloor\left(\mathrm{3}+{f}\right)\left(\mathrm{9}+\lfloor\mathrm{3}{f}\rfloor\right)\rfloor=\mathrm{88} \\ $$$$\left(\mathrm{3}+{f}\right)\lfloor\mathrm{27}+\mathrm{9}{f}+\mathrm{3}\lfloor\mathrm{3}{f}\rfloor+{f}\lfloor\mathrm{3}{f}\rfloor\rfloor=\mathrm{88} \\ $$$$\mathrm{81}+\mathrm{27}{f}+…=\mathrm{88} \\ $$$${f}<\frac{\mathrm{1}}{\mathrm{3}}\:\because\mathrm{27}×\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{9}>\mathrm{7}\:\Rightarrow\lfloor\mathrm{3}{f}\rfloor=\mathrm{0} \\ $$$$\left(\mathrm{3}+{f}\right)\lfloor\mathrm{27}+\mathrm{9}{f}\rfloor=\mathrm{88} \\ $$$$\mathrm{81}+\mathrm{27}{f}+{f}\lfloor\mathrm{9}{f}\rfloor+\mathrm{3}\lfloor\mathrm{9}{f}\rfloor=\mathrm{88} \\ $$$$\mathrm{27}{f}+{f}\lfloor\mathrm{9}{f}\rfloor+\mathrm{3}\lfloor\mathrm{9}{f}\rfloor=\mathrm{7} \\ $$$${x}<\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow\lfloor\mathrm{9}{f}\rfloor=\mathrm{2},\mathrm{1},\mathrm{0} \\ $$$$\lfloor\mathrm{9}{f}\rfloor=\mathrm{0}\Rightarrow{f}=\frac{\mathrm{7}}{\mathrm{27}}\:\:\Rightarrow\lfloor\mathrm{9}{f}\rfloor>\mathrm{0}\:\left({invalid}\right) \\ $$$$\lfloor\mathrm{9}{f}\rfloor=\mathrm{1}\Rightarrow{f}=\frac{\mathrm{1}}{\mathrm{7}}\:\Rightarrow\lfloor\mathrm{9}{f}\rfloor=\mathrm{1}\:\left({valid}\right) \\ $$$$\lfloor\mathrm{9}{f}\rfloor=\mathrm{2}\Rightarrow{f}=\frac{\mathrm{1}}{\mathrm{29}}\Rightarrow\lfloor\mathrm{9}{f}\rfloor=\mathrm{0}\:\left({invalid}\right) \\ $$$${x}=\mathrm{3}+{f}=\frac{\mathrm{22}}{\mathrm{7}} \\ $$
Commented by M±th+et+s last updated on 31/May/20
$${correct}\:{solution}\:{thank}\:{you} \\ $$
