Menu Close

x-x-x-x-find-x-

Tinku Tara 0 Comments
Pin




Question Number 175554 by Linton last updated on 02/Sep/22
x^(√x) =(√x^x ) find x
$${x}^{\sqrt{{x}}} =\sqrt{{x}^{{x}} } \\ $$$${find}\:{x} \\ $$
Answered by mr W last updated on 02/Sep/22
x=0 x^(x^(1/2) −(x/2)) =1 ⇒x=1 ⇒x^(1/2) −(x/2)=0 ⇒x=4
$${x}=\mathrm{0} \\ $$$${x}^{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} −\frac{{x}}{\mathrm{2}}} =\mathrm{1} \\ $$$$\Rightarrow{x}=\mathrm{1} \\ $$$$\Rightarrow{x}^{\frac{\mathrm{1}}{\mathrm{2}}} −\frac{{x}}{\mathrm{2}}=\mathrm{0}\:\Rightarrow{x}=\mathrm{4} \\ $$
Commented by BaliramKumar last updated on 02/Sep/22
x = 0 undefiend
$${x}\:=\:\mathrm{0}\:\mathrm{undefiend} \\ $$
Commented by mr W last updated on 02/Sep/22
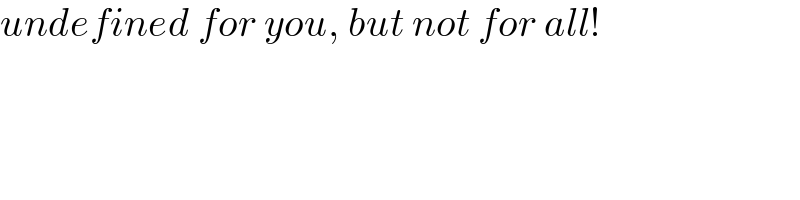
undefined for you, but not for all!
$${undefined}\:{for}\:{you},\:{but}\:{not}\:{for}\:{all}! \\ $$
Commented by mr W last updated on 02/Sep/22
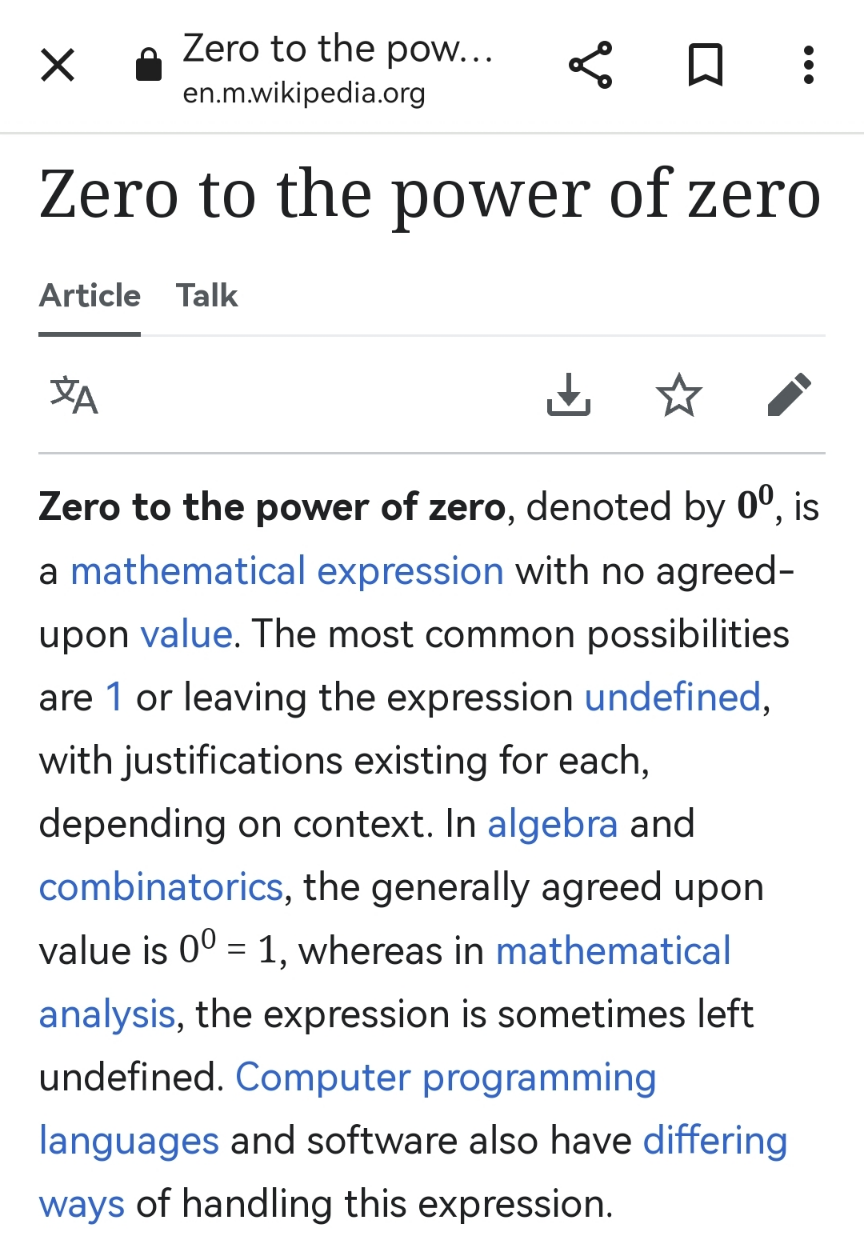
Commented by BaliramKumar last updated on 02/Sep/22
you are right sir 3 solution valid
$${you}\:{are}\:{right}\:{sir} \\ $$$$\mathrm{3}\:{solution}\:{valid} \\ $$
Commented by BaliramKumar last updated on 02/Sep/22
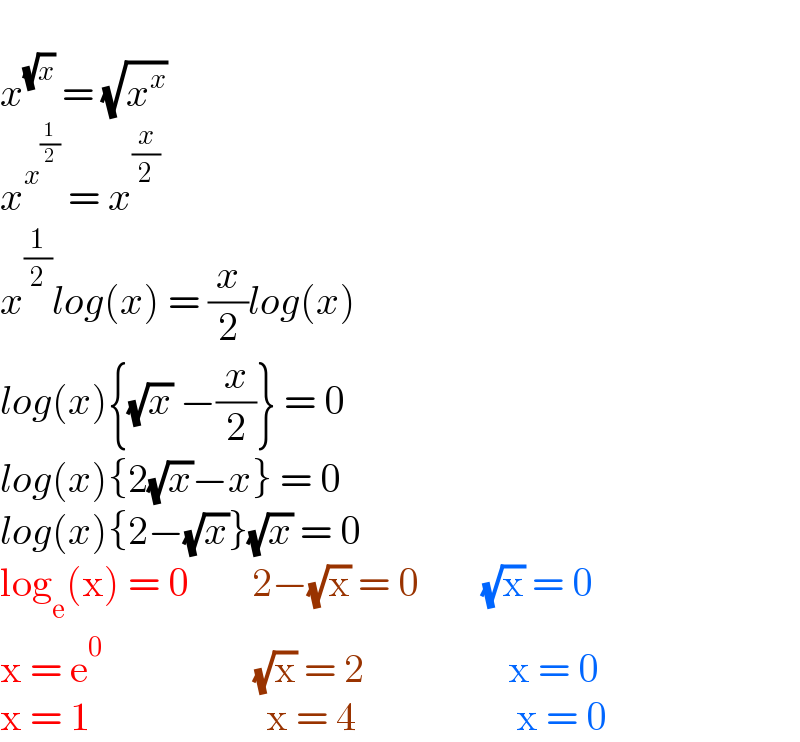
x^(√x) = (√x^x ) x^x^(1/2) = x^(x/2) x^(1/2) log(x) = (x/2)log(x) log(x){(√x) −(x/2)} = 0 log(x){2(√x)−x} = 0 log(x){2−(√x)}(√x) = 0 log_e (x) = 0 2−(√x) = 0 (√x) = 0 x = e^0 (√x) = 2 x = 0 x = 1 x = 4 x = 0
$$ \\ $$$${x}^{\sqrt{{x}}} \:=\:\sqrt{{x}^{{x}} } \\ $$$${x}^{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} } \:=\:{x}^{\frac{{x}}{\mathrm{2}}} \\ $$$${x}^{\frac{\mathrm{1}}{\mathrm{2}}} {log}\left({x}\right)\:=\:\frac{{x}}{\mathrm{2}}{log}\left({x}\right) \\ $$$${log}\left({x}\right)\left\{\sqrt{{x}}\:−\frac{{x}}{\mathrm{2}}\right\}\:=\:\mathrm{0} \\ $$$${log}\left({x}\right)\left\{\mathrm{2}\sqrt{{x}}−{x}\right\}\:=\:\mathrm{0} \\ $$$${log}\left({x}\right)\left\{\mathrm{2}−\sqrt{{x}}\right\}\sqrt{{x}}\:=\:\mathrm{0} \\ $$$$\mathrm{log}_{\mathrm{e}} \left(\mathrm{x}\right)\:=\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{2}−\sqrt{\mathrm{x}}\:=\:\mathrm{0}\:\:\:\:\:\:\:\:\sqrt{\mathrm{x}}\:=\:\mathrm{0} \\ $$$$\mathrm{x}\:=\:\mathrm{e}^{\mathrm{0}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{x}}\:=\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:=\:\mathrm{0} \\ $$$$\mathrm{x}\:=\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:=\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:=\:\mathrm{0} \\ $$
Commented by BaliramKumar last updated on 02/Sep/22
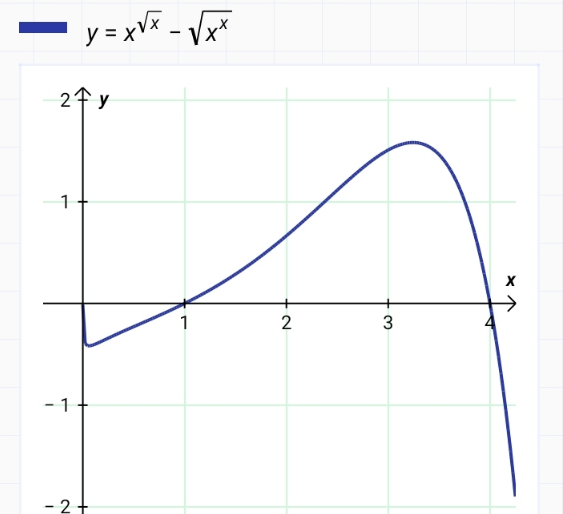
Answered by Rasheed.Sindhi last updated on 02/Sep/22
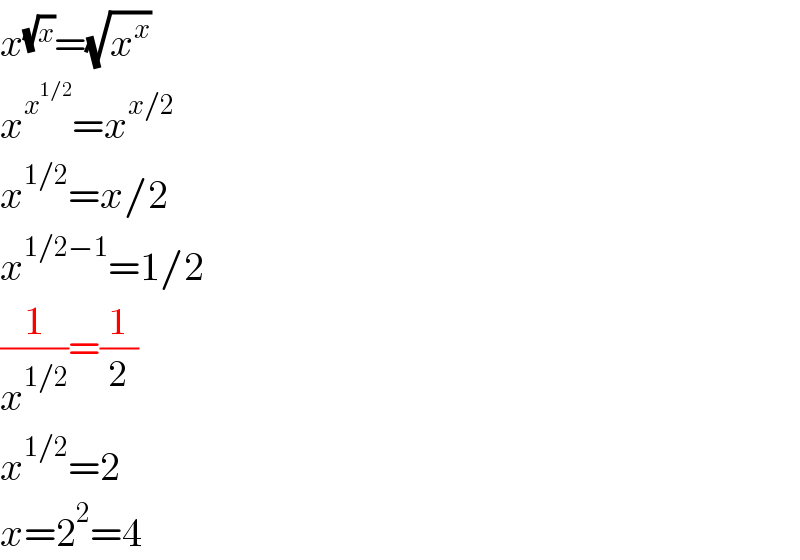
x^(√x) =(√x^x ) x^x^(1/2) =x^(x/2) x^(1/2) =x/2 x^(1/2−1) =1/2 (1/x^(1/2) )=(1/2) x^(1/2) =2 x=2^2 =4
$${x}^{\sqrt{{x}}} =\sqrt{{x}^{{x}} } \\ $$$${x}^{{x}^{\mathrm{1}/\mathrm{2}} } ={x}^{{x}/\mathrm{2}} \\ $$$${x}^{\mathrm{1}/\mathrm{2}} ={x}/\mathrm{2} \\ $$$${x}^{\mathrm{1}/\mathrm{2}−\mathrm{1}} =\mathrm{1}/\mathrm{2} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{1}/\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}^{\mathrm{1}/\mathrm{2}} =\mathrm{2} \\ $$$${x}=\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *