Question Number 102894 by bramlex last updated on 11/Jul/20
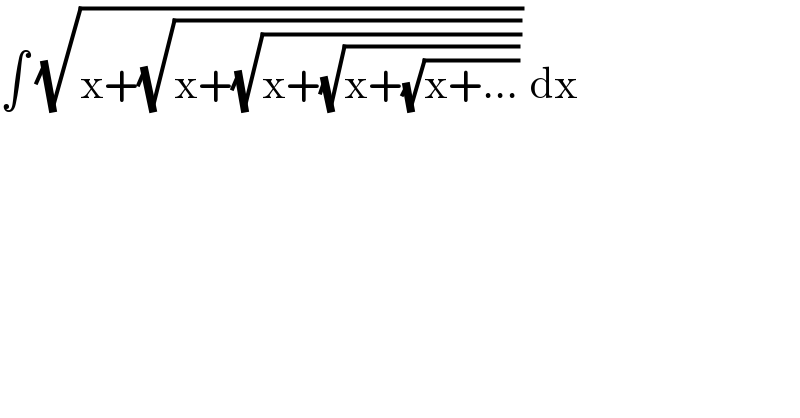
$$\int\:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+…}}}}}\:\mathrm{dx}\: \\ $$
Answered by bemath last updated on 11/Jul/20
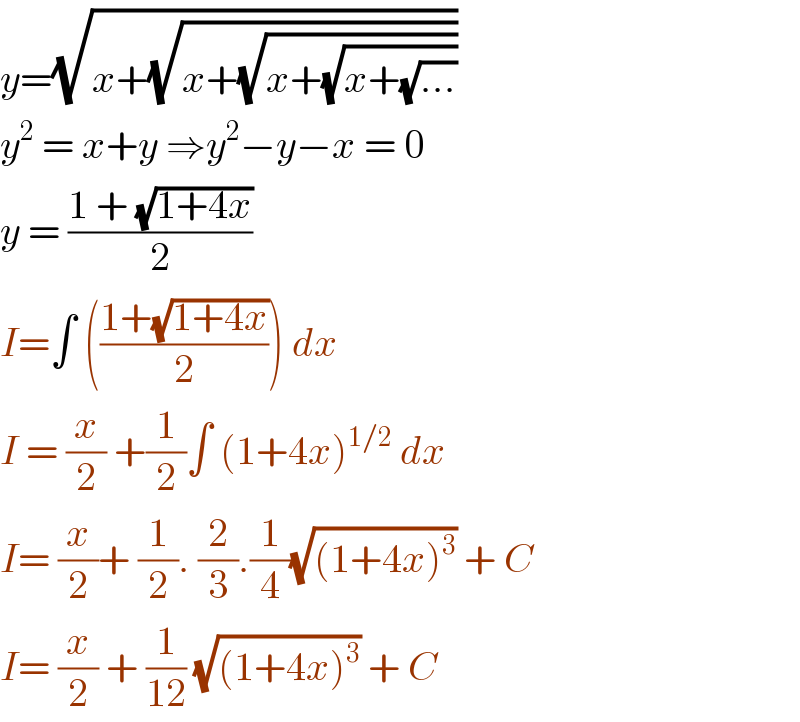
$${y}=\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{…}}}}}\: \\ $$$${y}^{\mathrm{2}} \:=\:{x}+{y}\:\Rightarrow{y}^{\mathrm{2}} −{y}−{x}\:=\:\mathrm{0} \\ $$$${y}\:=\:\frac{\mathrm{1}\:+\:\sqrt{\mathrm{1}+\mathrm{4}{x}}}{\mathrm{2}} \\ $$$${I}=\int\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{x}}}{\mathrm{2}}\right)\:{dx}\: \\ $$$${I}\:=\:\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{1}+\mathrm{4}{x}\right)^{\mathrm{1}/\mathrm{2}} \:{dx}\: \\ $$$${I}=\:\frac{{x}}{\mathrm{2}}+\:\frac{\mathrm{1}}{\mathrm{2}}.\:\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left(\mathrm{1}+\mathrm{4}{x}\right)^{\mathrm{3}} }\:+\:{C}\: \\ $$$${I}=\:\frac{{x}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{12}}\:\sqrt{\left(\mathrm{1}+\mathrm{4}{x}\right)^{\mathrm{3}} }\:+\:{C}\: \\ $$
Answered by Dwaipayan Shikari last updated on 11/Jul/20

$$\sqrt{{x}+\sqrt{{x}+\sqrt{{x}..}}}={y} \\ $$$${x}+{y}={y}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} −{y}−{x}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{x}}}{\mathrm{2}} \\ $$$$\int\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{x}}}{\mathrm{2}}=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{8}}\int\mathrm{4}\sqrt{\mathrm{1}+\mathrm{4}{x}}{dx}=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\int{u}^{\mathrm{2}} {du}\:\:\left({take}\:\sqrt{\mathrm{1}+\mathrm{4}{x}}={u}\right. \\ $$$$=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{12}}{u}^{\mathrm{3}} +{C}=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{12}}\left(\mathrm{1}+\mathrm{4}{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{Constant} \\ $$$${If}\:{it}\:{is} \\ $$$$\int\sqrt{{x}\sqrt{{x}\sqrt{{x}\sqrt{{x}\sqrt{{x}….\infty}}}}}{dx}=\int{y}=\int{xdx}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{C} \\ $$$${y}^{\mathrm{2}} ={xy} \\ $$$${y}^{\mathrm{2}} −{xy}=\mathrm{0}\:\:{y}=\mathrm{0}\:\:{or}\:{y}={x} \\ $$$$ \\ $$
Answered by Aziztisffola last updated on 11/Jul/20

