Menu Close

x-x-y-y-31-x-y-5-Find-x-and-y-

Tinku Tara 0 Comments
Pin




Question Number 42906 by Cheyboy last updated on 04/Sep/18
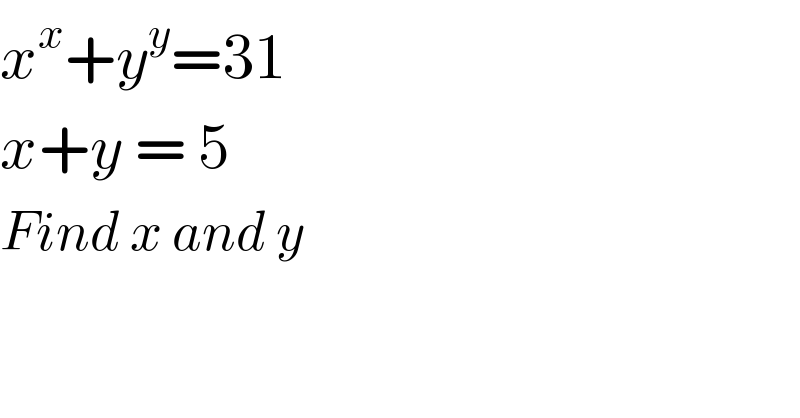
x^x +y^y =31 x+y = 5 Find x and y
$${x}^{{x}} +{y}^{{y}} =\mathrm{31} \\ $$$${x}+{y}\:=\:\mathrm{5} \\ $$$${Find}\:{x}\:{and}\:{y} \\ $$
Answered by Joel578 last updated on 04/Sep/18
∴ (x, y) = (3, 2), (2, 3)
$$\therefore\:\left({x},\:{y}\right)\:=\:\left(\mathrm{3},\:\mathrm{2}\right),\:\left(\mathrm{2},\:\mathrm{3}\right) \\ $$
Commented by Cheyboy last updated on 04/Sep/18
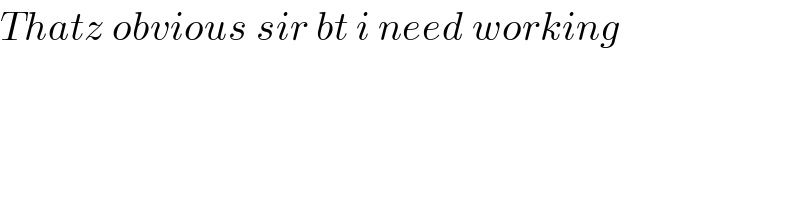
Thatz obvious sir bt i need working
$${Thatz}\:{obvious}\:{sir}\:{bt}\:{i}\:{need}\:{working} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Sep/18
solve by reasoning x y x^x y^y x^x +y^y remarks 1 4 1 256 257 not satisfy 2 3 4 27 31 satisfy 3 2 27 4 31 satisfy 4 1 256 1 257 not satisfy hence two set of solution x=2 y=3 x=3 y=2
$${solve}\:{by}\:{reasoning} \\ $$$${x}\:\:\:\:\:{y}\:\:\:\:\:\:\:{x}^{{x}} \:\:\:\:\:\:{y}^{{y}} \:\:\:\:\:\:{x}^{{x}} +{y}^{{y}} \:\:\:\:\:\:\:{remarks} \\ $$$$\mathrm{1}\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{256}\:\:\:\:\:\mathrm{257}\:\:\:\:\:\:\:\:\:\:\:{not}\:{satisfy} \\ $$$$\mathrm{2}\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\mathrm{27}\:\:\:\:\:\:\:\:\:\:\mathrm{31}\:\:\:\:\:\:\:\:\:\:\:{satisfy} \\ $$$$\mathrm{3}\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{27}\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{31}\:\:\:\:\:\:\:\:\:{satisfy} \\ $$$$\mathrm{4}\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{256}\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{257}\:\:\:\:\:\:\:{not}\:{satisfy} \\ $$$${hence}\:{two}\:{set}\:{of}\:{solution} \\ $$$${x}=\mathrm{2}\:\:\:{y}=\mathrm{3} \\ $$$${x}=\mathrm{3}\:\:\:\:{y}=\mathrm{2} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 04/Sep/18
Answered by MJS last updated on 05/Sep/18
y=5−x x^x +(5−x)^(5−x) −31=0 put f(x)=x^x +(5−x)^(5−x) −31 this is symmetric: set x → (5−x) and f(x) stays the same ⇒ minimum at (((5/2)),((−31+((25(√(10)))/4))) ) we can only approximate zeros and find x_1 =2; x_2 =3 f′(x)=(1+ln x)x^x −(1+ln (5−x))(5−x)^(5−x) it′s easy to see that f′((5/2))=0 and x<(5/2) ⇒ f′(x)<0; x>(5/2) ⇒ f′(x)>0 ⇒ no other solutions ∈R
$${y}=\mathrm{5}−{x} \\ $$$${x}^{{x}} +\left(\mathrm{5}−{x}\right)^{\mathrm{5}−{x}} −\mathrm{31}=\mathrm{0} \\ $$$$\mathrm{put}\:{f}\left({x}\right)={x}^{{x}} +\left(\mathrm{5}−{x}\right)^{\mathrm{5}−{x}} −\mathrm{31} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{symmetric}: \\ $$$$\mathrm{set}\:{x}\:\rightarrow\:\left(\mathrm{5}−{x}\right)\:\mathrm{and}\:{f}\left({x}\right)\:\mathrm{stays}\:\mathrm{the}\:\mathrm{same} \\ $$$$\Rightarrow\:\mathrm{minimum}\:\mathrm{at}\:\begin{pmatrix}{\frac{\mathrm{5}}{\mathrm{2}}}\\{−\mathrm{31}+\frac{\mathrm{25}\sqrt{\mathrm{10}}}{\mathrm{4}}}\end{pmatrix} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{approximate}\:\mathrm{zeros}\:\mathrm{and}\:\mathrm{find} \\ $$$${x}_{\mathrm{1}} =\mathrm{2};\:{x}_{\mathrm{2}} =\mathrm{3} \\ $$$$ \\ $$$${f}'\left({x}\right)=\left(\mathrm{1}+\mathrm{ln}\:{x}\right){x}^{{x}} −\left(\mathrm{1}+\mathrm{ln}\:\left(\mathrm{5}−{x}\right)\right)\left(\mathrm{5}−{x}\right)^{\mathrm{5}−{x}} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:{f}'\left(\frac{\mathrm{5}}{\mathrm{2}}\right)=\mathrm{0}\:\mathrm{and} \\ $$$${x}<\frac{\mathrm{5}}{\mathrm{2}}\:\Rightarrow\:{f}'\left({x}\right)<\mathrm{0};\:{x}>\frac{\mathrm{5}}{\mathrm{2}}\:\Rightarrow\:{f}'\left({x}\right)>\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{other}\:\mathrm{solutions}\:\in\mathbb{R} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *