Menu Close

x-y-1-8-x-1-4-y-1-4-1-solve-system-

Tinku Tara 0 Comments
Pin




Question Number 14742 by Mr Chheang Chantria last updated on 04/Jun/17
x+y=(1/8) (x)^(1/4) +(y)^(1/4) =1 solve system
$$\boldsymbol{{x}}+\boldsymbol{{y}}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\sqrt[{\mathrm{4}}]{\boldsymbol{{x}}}+\sqrt[{\mathrm{4}}]{\boldsymbol{{y}}}=\mathrm{1} \\ $$$$\boldsymbol{{solve}}\:\boldsymbol{{system}} \\ $$
Commented by Tinkutara last updated on 04/Jun/17
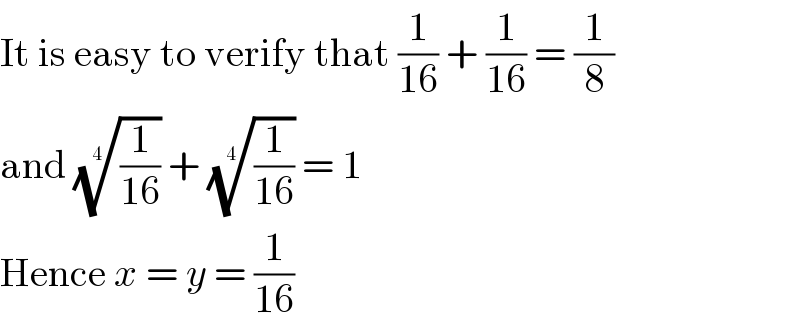
It is easy to verify that (1/(16)) + (1/(16)) = (1/8) and ((1/(16)))^(1/4) + ((1/(16)))^(1/4) = 1 Hence x = y = (1/(16))
$$\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{verify}\:\mathrm{that}\:\frac{\mathrm{1}}{\mathrm{16}}\:+\:\frac{\mathrm{1}}{\mathrm{16}}\:=\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{and}\:\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}}{\mathrm{16}}}\:+\:\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}}{\mathrm{16}}}\:=\:\mathrm{1} \\ $$$$\mathrm{Hence}\:{x}\:=\:{y}\:=\:\frac{\mathrm{1}}{\mathrm{16}} \\ $$
Commented by RasheedSoomro last updated on 04/Jun/17
Let (x)^(1/4) =p and (y)^(1/4) =q ⇒ { ((p^4 +q^4 =1/8)),((p+q=1)) :} ⇒((p^4 +q^4 )/(p+q))=(1/8) ∧ (p^4 +q^4 )(p+q)=(1/8) ⇒((p^4 +q^4 )/(p+q))− (p^4 +q^4 )(p+q)=0 ⇒(p^4 +q^4 ){(1/(p+q))−(p+q)}=0 p^4 +q^4 =0 ∨ p+q− (1/(p+q))=0 p^4 =−q^4 ∨ p+q= (1/(p+q)) x=−y ∨ (p+q)^2 = 1 p+q= ±1 p+q=1 is what we have been given! hahahaa.. I reached at the starting point again!!! p+q=−1 is extraneous(?) Oh no I′ve gained something x=−y But this is again in contradiction to the given (x+y=1/8) !!! Continue
$$\mathrm{Let}\:\sqrt[{\mathrm{4}}]{\boldsymbol{{x}}}=\mathrm{p}\:\mathrm{and}\:\sqrt[{\mathrm{4}}]{{y}}=\mathrm{q} \\ $$$$\Rightarrow\begin{cases}{\mathrm{p}^{\mathrm{4}} +\mathrm{q}^{\mathrm{4}} =\mathrm{1}/\mathrm{8}}\\{\mathrm{p}+\mathrm{q}=\mathrm{1}}\end{cases} \\ $$$$\Rightarrow\frac{\mathrm{p}^{\mathrm{4}} +\mathrm{q}^{\mathrm{4}} }{\mathrm{p}+\mathrm{q}}=\frac{\mathrm{1}}{\mathrm{8}}\:\wedge\:\left(\mathrm{p}^{\mathrm{4}} +\mathrm{q}^{\mathrm{4}} \right)\left(\mathrm{p}+\mathrm{q}\right)=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\Rightarrow\frac{\mathrm{p}^{\mathrm{4}} +\mathrm{q}^{\mathrm{4}} }{\mathrm{p}+\mathrm{q}}−\:\left(\mathrm{p}^{\mathrm{4}} +\mathrm{q}^{\mathrm{4}} \right)\left(\mathrm{p}+\mathrm{q}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{p}^{\mathrm{4}} +\mathrm{q}^{\mathrm{4}} \right)\left\{\frac{\mathrm{1}}{\mathrm{p}+\mathrm{q}}−\left(\mathrm{p}+\mathrm{q}\right)\right\}=\mathrm{0} \\ $$$$\mathrm{p}^{\mathrm{4}} +\mathrm{q}^{\mathrm{4}} =\mathrm{0}\:\vee\:\mathrm{p}+\mathrm{q}−\:\frac{\mathrm{1}}{\mathrm{p}+\mathrm{q}}=\mathrm{0} \\ $$$$\mathrm{p}^{\mathrm{4}} =−\mathrm{q}^{\mathrm{4}} \:\vee\:\mathrm{p}+\mathrm{q}=\:\frac{\mathrm{1}}{\mathrm{p}+\mathrm{q}} \\ $$$$\mathrm{x}=−\mathrm{y}\:\:\vee\:\left(\mathrm{p}+\mathrm{q}\right)^{\mathrm{2}} =\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{p}+\mathrm{q}=\:\pm\mathrm{1} \\ $$$$\mathrm{p}+\mathrm{q}=\mathrm{1}\:\mathrm{is}\:\mathrm{what}\:\mathrm{we}\:\mathrm{have}\:\mathrm{been}\:\mathrm{given}!\:\mathrm{hahahaa}.. \\ $$$$\mathrm{I}\:\mathrm{reached}\:\mathrm{at}\:\mathrm{the}\:\mathrm{starting}\:\mathrm{point}\:\mathrm{again}!!! \\ $$$$\mathrm{p}+\mathrm{q}=−\mathrm{1}\:\mathrm{is}\:\mathrm{extraneous}\left(?\right) \\ $$$$ \\ $$$$\mathrm{Oh}\:\mathrm{no}\:\mathrm{I}'\mathrm{ve}\:\mathrm{gained}\:\mathrm{something}\:\mathrm{x}=−\mathrm{y} \\ $$$$\mathrm{But}\:\mathrm{this}\:\mathrm{is}\:\mathrm{again}\:\:\mathrm{in}\:\mathrm{contradiction}\:\mathrm{to}\:\mathrm{the}\:\mathrm{given} \\ $$$$\left(\mathrm{x}+\mathrm{y}=\mathrm{1}/\mathrm{8}\right) \\ $$$$!!! \\ $$$$\mathrm{Continue} \\ $$
Commented by prakash jain last updated on 04/Jun/17
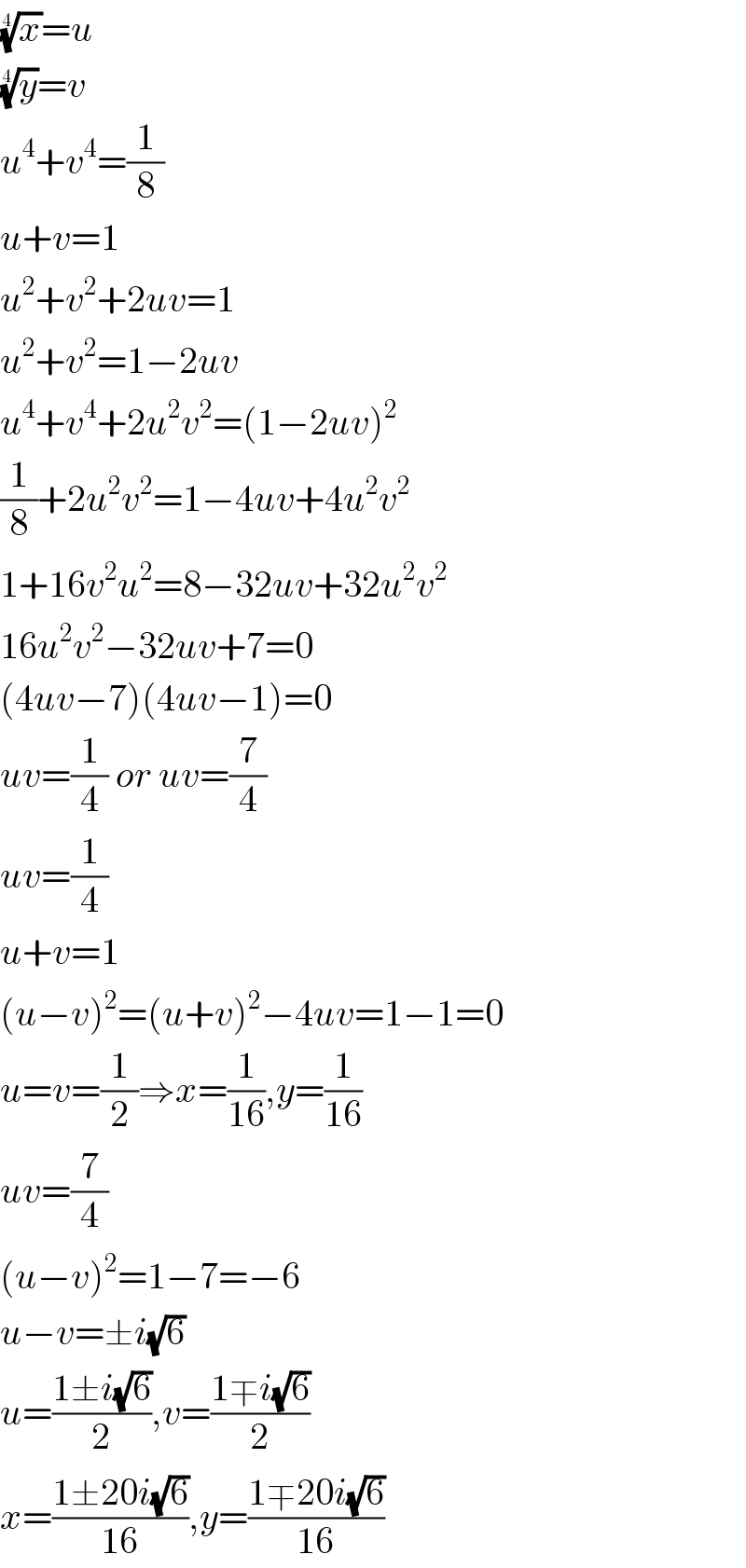
(x)^(1/4) =u (y)^(1/4) =v u^4 +v^4 =(1/8) u+v=1 u^2 +v^2 +2uv=1 u^2 +v^2 =1−2uv u^4 +v^4 +2u^2 v^2 =(1−2uv)^2 (1/8)+2u^2 v^2 =1−4uv+4u^2 v^2 1+16v^2 u^2 =8−32uv+32u^2 v^2 16u^2 v^2 −32uv+7=0 (4uv−7)(4uv−1)=0 uv=(1/4) or uv=(7/4) uv=(1/4) u+v=1 (u−v)^2 =(u+v)^2 −4uv=1−1=0 u=v=(1/2)⇒x=(1/(16)),y=(1/(16)) uv=(7/4) (u−v)^2 =1−7=−6 u−v=±i(√6) u=((1±i(√6))/2),v=((1∓i(√6))/2) x=((1±20i(√6))/(16)),y=((1∓20i(√6))/(16))
$$\sqrt[{\mathrm{4}}]{{x}}={u} \\ $$$$\sqrt[{\mathrm{4}}]{{y}}={v} \\ $$$${u}^{\mathrm{4}} +{v}^{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${u}+{v}=\mathrm{1} \\ $$$${u}^{\mathrm{2}} +{v}^{\mathrm{2}} +\mathrm{2}{uv}=\mathrm{1} \\ $$$${u}^{\mathrm{2}} +{v}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}{uv} \\ $$$${u}^{\mathrm{4}} +{v}^{\mathrm{4}} +\mathrm{2}{u}^{\mathrm{2}} {v}^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{2}{uv}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{8}}+\mathrm{2}{u}^{\mathrm{2}} {v}^{\mathrm{2}} =\mathrm{1}−\mathrm{4}{uv}+\mathrm{4}{u}^{\mathrm{2}} {v}^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{16}{v}^{\mathrm{2}} {u}^{\mathrm{2}} =\mathrm{8}−\mathrm{32}{uv}+\mathrm{32}{u}^{\mathrm{2}} {v}^{\mathrm{2}} \\ $$$$\mathrm{16}{u}^{\mathrm{2}} {v}^{\mathrm{2}} −\mathrm{32}{uv}+\mathrm{7}=\mathrm{0} \\ $$$$\left(\mathrm{4}{uv}−\mathrm{7}\right)\left(\mathrm{4}{uv}−\mathrm{1}\right)=\mathrm{0} \\ $$$${uv}=\frac{\mathrm{1}}{\mathrm{4}}\:{or}\:{uv}=\frac{\mathrm{7}}{\mathrm{4}} \\ $$$${uv}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${u}+{v}=\mathrm{1} \\ $$$$\left({u}−{v}\right)^{\mathrm{2}} =\left({u}+{v}\right)^{\mathrm{2}} −\mathrm{4}{uv}=\mathrm{1}−\mathrm{1}=\mathrm{0} \\ $$$${u}={v}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{16}},{y}=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$${uv}=\frac{\mathrm{7}}{\mathrm{4}} \\ $$$$\left({u}−{v}\right)^{\mathrm{2}} =\mathrm{1}−\mathrm{7}=−\mathrm{6} \\ $$$${u}−{v}=\pm{i}\sqrt{\mathrm{6}} \\ $$$${u}=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{6}}}{\mathrm{2}},{v}=\frac{\mathrm{1}\mp{i}\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{1}\pm\mathrm{20}{i}\sqrt{\mathrm{6}}}{\mathrm{16}},{y}=\frac{\mathrm{1}\mp\mathrm{20}{i}\sqrt{\mathrm{6}}}{\mathrm{16}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *