Question Number 104357 by bemath last updated on 21/Jul/20
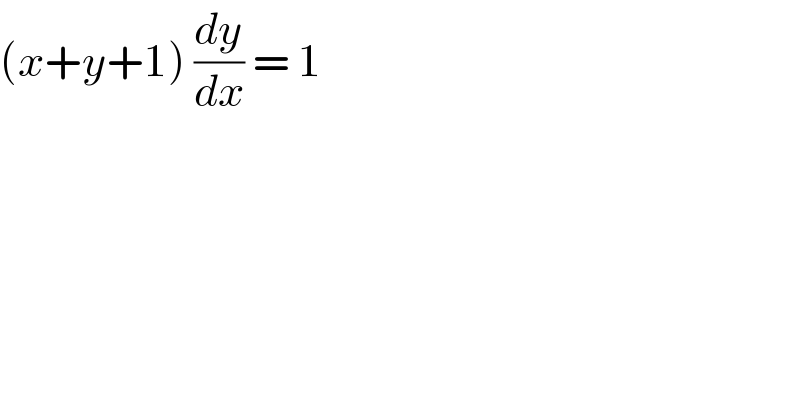
$$\left({x}+{y}+\mathrm{1}\right)\:\frac{{dy}}{{dx}}\:=\:\mathrm{1}\: \\ $$
Answered by john santu last updated on 21/Jul/20

$${let}\:{z}\:=\:{x}+{y}+\mathrm{1} \\ $$$$\frac{{dz}}{{dx}}\:=\:\mathrm{1}+\:\frac{{dy}}{{dx}}\:\Rightarrow\frac{{dy}}{{dx}}\:=\:\frac{{dz}}{{dx}}−\mathrm{1} \\ $$$$\left(\rightarrow\right)\:{z}.\left(\frac{{dz}}{{dx}}−\mathrm{1}\right)\:=\:\mathrm{1}\: \\ $$$$\left(\rightarrow\right)\:\frac{{dz}}{{dx}}\:=\:\frac{\mathrm{1}}{{z}}+\mathrm{1} \\ $$$$\left(\rightarrow\right)\:\frac{{dz}}{{dx}}\:=\:\frac{\mathrm{1}+{z}}{{z}}\:;\:\frac{{z}\:{dz}}{\mathrm{1}+{z}}\:=\:{dx} \\ $$$$\left(\rightarrow\right)\:\int\:\frac{\left(\mathrm{1}+{z}−\mathrm{1}\right){dz}}{\mathrm{1}+{z}}\:=\:{x}\:+{C} \\ $$$$\left(\rightarrow\right)\:\int\:{dz}\:−\int\:\frac{{dz}}{{z}+\mathrm{1}}\:=\:{x}\:+{C}\: \\ $$$${z}−\:\mathrm{ln}\:\mid{z}+\mathrm{1}\mid\:=\:{x}\:+{C} \\ $$$$\therefore\:{x}+{y}+\mathrm{1}−\mathrm{ln}\:\mid{x}+{y}+\mathrm{2}\mid\:=\:{x}+{C} \\ $$$${y}\:−\:\mathrm{ln}\:\mid{x}+{y}+\mathrm{2}\mid\:=\:{K}\: \\ $$$$\left({JS}\:\circledast\right) \\ $$
Answered by OlafThorendsen last updated on 21/Jul/20

$${x}+{y}+\mathrm{1}\:=\:\frac{{dx}}{{dy}} \\ $$$$\frac{{dx}}{{dy}}−{x}\:=\:{y}+\mathrm{1} \\ $$$${x}_{\mathrm{P}} \:=\:−{y}+{b} \\ $$$$\Rightarrow\:−\mathrm{1}+{y}−{b}\:=\:{y}+\mathrm{1} \\ $$$${b}\:=\:−\mathrm{2} \\ $$$${x}_{\mathrm{P}} \:=\:−{y}−\mathrm{2} \\ $$$$\frac{{dx}_{\mathrm{H}} }{{dy}}−{x}_{\mathrm{H}} \:=\:\mathrm{0} \\ $$$$\frac{{dx}_{\mathrm{H}} }{{x}_{\mathrm{H}} }\:=\:{dy} \\ $$$$\mathrm{ln}\mid{x}_{\mathrm{H}} \mid\:=\:{y}+\mathrm{C} \\ $$$${x}_{\mathrm{H}} \:=\:\mathrm{K}{e}^{{y}} \\ $$$$\mathrm{Finally}\:{x}\:=\:{x}_{\mathrm{P}} +{x}_{\mathrm{H}} \:=\:\mathrm{K}{e}^{{y}} −{y}−\mathrm{2} \\ $$$$\mathrm{In}\:\mathrm{this}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{probem} \\ $$$${x}\:=\:{x}\left({y}\right)\:\mathrm{is}\:\mathrm{better}\:\mathrm{than}\:{y}\:=\:{y}\left({x}\right) \\ $$$$ \\ $$
