Question Number 87614 by mary_ last updated on 05/Apr/20
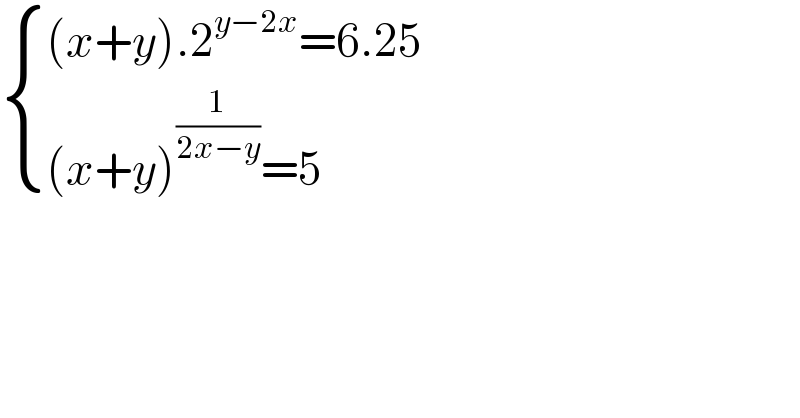
$$\begin{cases}{\left({x}+{y}\right).\mathrm{2}^{{y}−\mathrm{2}{x}} =\mathrm{6}.\mathrm{25}}\\{\left({x}+{y}\right)^{\frac{\mathrm{1}}{\mathrm{2}{x}−{y}}} =\mathrm{5}}\end{cases} \\ $$
Answered by mahdi last updated on 05/Apr/20
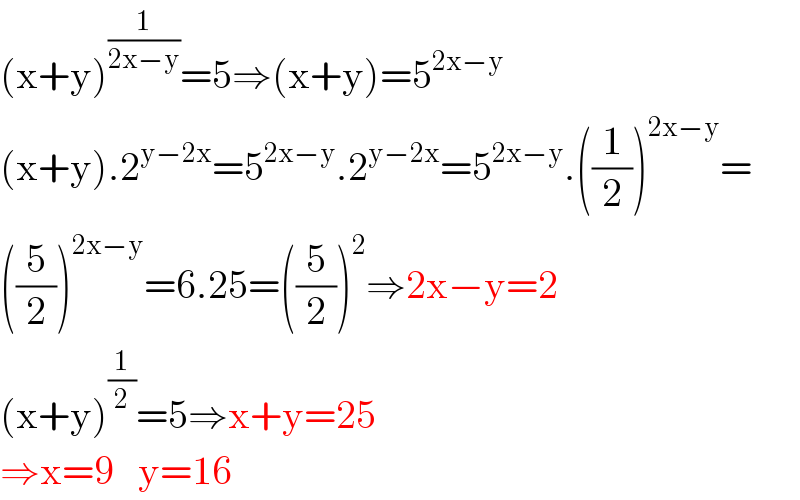
$$\left(\mathrm{x}+\mathrm{y}\right)^{\frac{\mathrm{1}}{\mathrm{2x}−\mathrm{y}}} =\mathrm{5}\Rightarrow\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{5}^{\mathrm{2x}−\mathrm{y}} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right).\mathrm{2}^{\mathrm{y}−\mathrm{2x}} =\mathrm{5}^{\mathrm{2x}−\mathrm{y}} .\mathrm{2}^{\mathrm{y}−\mathrm{2x}} =\mathrm{5}^{\mathrm{2x}−\mathrm{y}} .\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2x}−\mathrm{y}} = \\ $$$$\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2x}−\mathrm{y}} =\mathrm{6}.\mathrm{25}=\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} \Rightarrow\mathrm{2x}−\mathrm{y}=\mathrm{2} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{5}\Rightarrow\mathrm{x}+\mathrm{y}=\mathrm{25} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{9}\:\:\:\mathrm{y}=\mathrm{16} \\ $$
