Question Number 89994 by jagoll last updated on 20/Apr/20
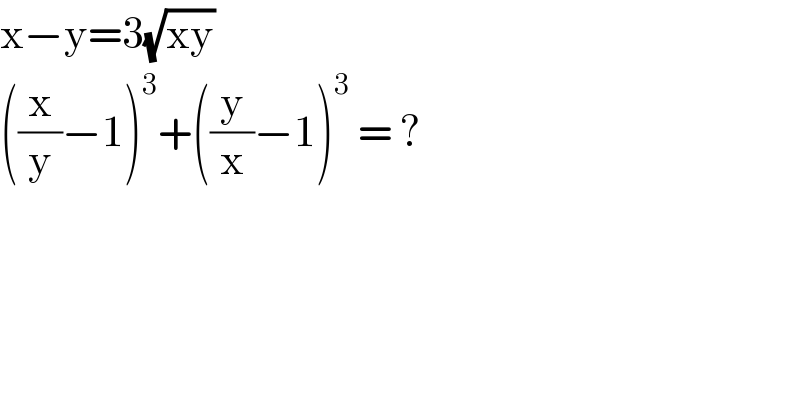
$$\mathrm{x}−\mathrm{y}=\mathrm{3}\sqrt{\mathrm{xy}} \\ $$$$\left(\frac{\mathrm{x}}{\mathrm{y}}−\mathrm{1}\right)^{\mathrm{3}} +\left(\frac{\mathrm{y}}{\mathrm{x}}−\mathrm{1}\right)^{\mathrm{3}} \:=\:? \\ $$
Answered by MJS last updated on 21/Apr/20
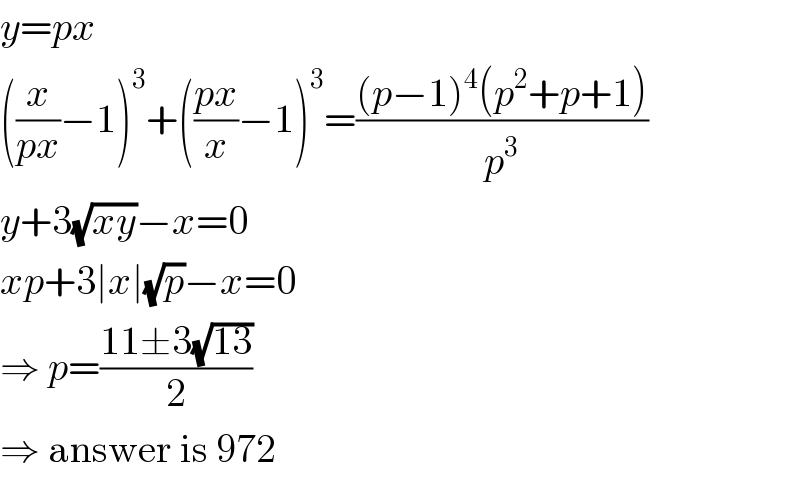
$${y}={px} \\ $$$$\left(\frac{{x}}{{px}}−\mathrm{1}\right)^{\mathrm{3}} +\left(\frac{{px}}{{x}}−\mathrm{1}\right)^{\mathrm{3}} =\frac{\left({p}−\mathrm{1}\right)^{\mathrm{4}} \left({p}^{\mathrm{2}} +{p}+\mathrm{1}\right)}{{p}^{\mathrm{3}} } \\ $$$${y}+\mathrm{3}\sqrt{{xy}}−{x}=\mathrm{0} \\ $$$${xp}+\mathrm{3}\mid{x}\mid\sqrt{{p}}−{x}=\mathrm{0} \\ $$$$\Rightarrow\:{p}=\frac{\mathrm{11}\pm\mathrm{3}\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{972} \\ $$
Answered by john santu last updated on 21/Apr/20
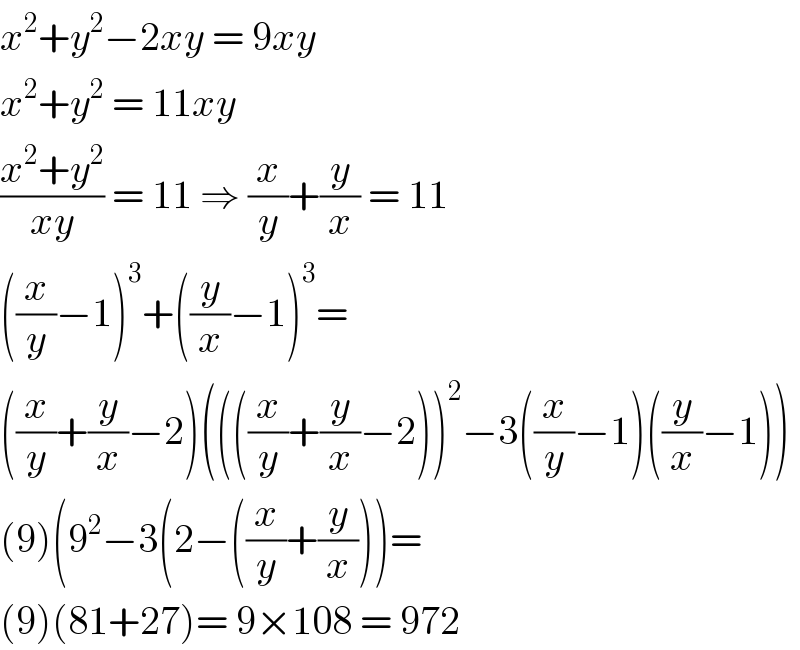
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{xy}\:=\:\mathrm{9}{xy} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:=\:\mathrm{11}{xy}\: \\ $$$$\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{{xy}}\:=\:\mathrm{11}\:\Rightarrow\:\frac{{x}}{{y}}+\frac{{y}}{{x}}\:=\:\mathrm{11} \\ $$$$\left(\frac{{x}}{{y}}−\mathrm{1}\right)^{\mathrm{3}} +\left(\frac{{y}}{{x}}−\mathrm{1}\right)^{\mathrm{3}} =\: \\ $$$$\left(\frac{{x}}{{y}}+\frac{{y}}{{x}}−\mathrm{2}\right)\left(\left(\left(\frac{{x}}{{y}}+\frac{{y}}{{x}}−\mathrm{2}\right)\right)^{\mathrm{2}} −\mathrm{3}\left(\frac{{x}}{{y}}−\mathrm{1}\right)\left(\frac{{y}}{{x}}−\mathrm{1}\right)\right) \\ $$$$\left(\mathrm{9}\right)\left(\mathrm{9}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{2}−\left(\frac{{x}}{{y}}+\frac{{y}}{{x}}\right)\right)=\right. \\ $$$$\left(\mathrm{9}\right)\left(\mathrm{81}+\mathrm{27}\right)=\:\mathrm{9}×\mathrm{108}\:=\:\mathrm{972} \\ $$
