x-y-5pi-3-sin-x-2sin-y-

Question Number 125359 by weltr last updated on 10/Dec/20

{ ((x + y = ((5π)/3))),((sin x = 2sin y)) :}

$$\begin{cases}{{x}\:+\:{y}\:=\:\frac{\mathrm{5}\pi}{\mathrm{3}}}\\{{sin}\:{x}\:=\:\mathrm{2}{sin}\:{y}}\end{cases} \\ $$

Answered by Ar Brandon last updated on 10/Dec/20

{ ((x+y=((5π)/3)),(...(i))),((sinx=2siny),(...(ii))) :} From (i), x+y=((5π)/3) ⇒ y=((5π)/3)−x substituting the above result in (ii) we have ; sinx=2sin(((5π)/3)−x)=2sin(π+(((2π)/3)−x))=2sin(x−((2π)/3)) {sin(π+x)=−sinx=sin(−x)} =2[sin(x)cos(((2π)/3))−cos(x)sin(((2π)/3))] =2[−(1/2)sinx−((√3)/2)cosx]=−sinx−(√3)cosx ⇒2sinx=−(√3)cosx ⇒ tanx=−((√3)/2) x=tan^(−1) (−((√3)/2)) , y=((5π)/3)−tan^(−1) (−((√3)/2))

$$\begin{cases}{\mathrm{x}+\mathrm{y}=\frac{\mathrm{5}\pi}{\mathrm{3}}}&{…\left(\mathrm{i}\right)}\\{\mathrm{sinx}=\mathrm{2siny}}&{…\left(\mathrm{ii}\right)}\end{cases} \\ $$$$\mathrm{From}\:\left(\mathrm{i}\right),\:\mathrm{x}+\mathrm{y}=\frac{\mathrm{5}\pi}{\mathrm{3}}\:\Rightarrow\:\mathrm{y}=\frac{\mathrm{5}\pi}{\mathrm{3}}−\mathrm{x} \\ $$$$\mathrm{substituting}\:\mathrm{the}\:\mathrm{above}\:\mathrm{result}\:\mathrm{in}\:\left(\mathrm{ii}\right)\:\mathrm{we}\:\mathrm{have}\:; \\ $$$$\mathrm{sinx}=\mathrm{2sin}\left(\frac{\mathrm{5}\pi}{\mathrm{3}}−\mathrm{x}\right)=\mathrm{2sin}\left(\pi+\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\mathrm{x}\right)\right)=\mathrm{2sin}\left(\mathrm{x}−\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left\{{sin}\left(\pi+{x}\right)=−{sinx}={sin}\left(−{x}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{2}\left[\mathrm{sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)−\mathrm{cos}\left(\mathrm{x}\right)\mathrm{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{2}\left[−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinx}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cosx}\right]=−\mathrm{sinx}−\sqrt{\mathrm{3}}\mathrm{cosx} \\ $$$$\Rightarrow\mathrm{2sinx}=−\sqrt{\mathrm{3}}\mathrm{cosx}\:\Rightarrow\:\mathrm{tanx}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{x}=\mathrm{tan}^{−\mathrm{1}} \left(−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:,\:\mathrm{y}=\frac{\mathrm{5}\pi}{\mathrm{3}}−\mathrm{tan}^{−\mathrm{1}} \left(−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$

Commented by MJS_new last updated on 10/Dec/20

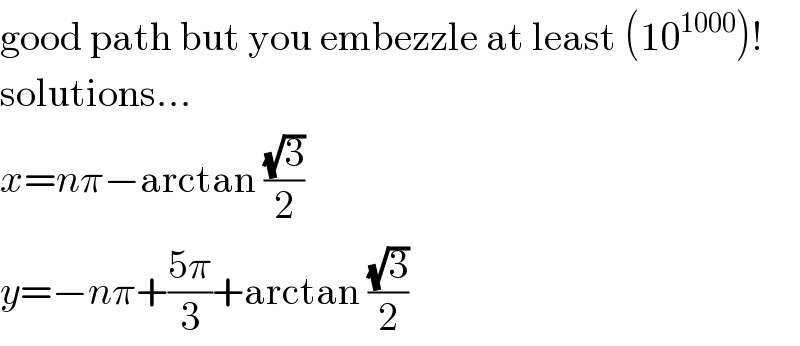
good path but you embezzle at least (10^(1000) )! solutions... x=nπ−arctan ((√3)/2) y=−nπ+((5π)/3)+arctan ((√3)/2)

$$\mathrm{good}\:\mathrm{path}\:\mathrm{but}\:\mathrm{you}\:\mathrm{embezzle}\:\mathrm{at}\:\mathrm{least}\:\left(\mathrm{10}^{\mathrm{1000}} \right)! \\ $$$$\mathrm{solutions}… \\ $$$${x}={n}\pi−\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${y}=−{n}\pi+\frac{\mathrm{5}\pi}{\mathrm{3}}+\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$