x-y-6-y-z-10-x-y-z-gt-0-

Question Number 50279 by Saorey last updated on 15/Dec/18

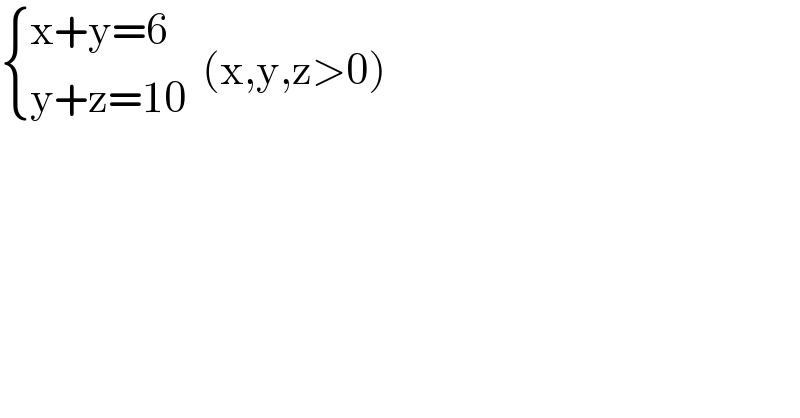
$$\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{6}}\\{\mathrm{y}+\mathrm{z}=\mathrm{10}}\end{cases}\:\:\left(\mathrm{x},\mathrm{y},\mathrm{z}>\mathrm{0}\right) \\ $$

Answered by mr W last updated on 15/Dec/18

if x,y,z are integers,then (x,y,z)=(1,5,5)/(2,4,6)/(3,3,7)/(4,2,8)/(5,1,9) if x,y,z are real, then x=6−a y=a z=10−a with 0<a<6

$${if}\:{x},{y},{z}\:{are}\:{integers},{then} \\ $$$$\left({x},{y},{z}\right)=\left(\mathrm{1},\mathrm{5},\mathrm{5}\right)/\left(\mathrm{2},\mathrm{4},\mathrm{6}\right)/\left(\mathrm{3},\mathrm{3},\mathrm{7}\right)/\left(\mathrm{4},\mathrm{2},\mathrm{8}\right)/\left(\mathrm{5},\mathrm{1},\mathrm{9}\right) \\ $$$${if}\:{x},{y},{z}\:{are}\:{real},\:{then} \\ $$$${x}=\mathrm{6}−{a} \\ $$$${y}={a} \\ $$$${z}=\mathrm{10}−{a} \\ $$$${with}\:\mathrm{0}<{a}<\mathrm{6} \\ $$

Answered by Rasheed.Sindhi last updated on 15/Dec/18

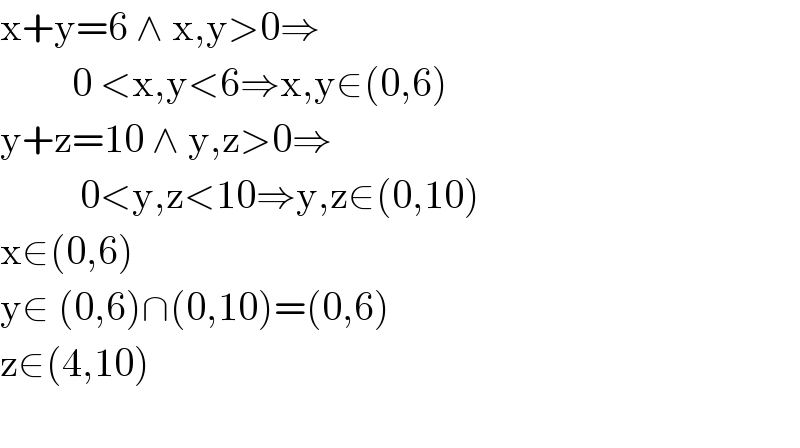
x+y=6 ∧ x,y>0⇒ 0 <x,y<6⇒x,y∈(0,6) y+z=10 ∧ y,z>0⇒ 0<y,z<10⇒y,z∈(0,10) x∈(0,6) y∈ (0,6)∩(0,10)=(0,6) z∈(4,10)

$$\mathrm{x}+\mathrm{y}=\mathrm{6}\:\wedge\:\mathrm{x},\mathrm{y}>\mathrm{0}\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{0}\:<\mathrm{x},\mathrm{y}<\mathrm{6}\Rightarrow\mathrm{x},\mathrm{y}\in\left(\mathrm{0},\mathrm{6}\right) \\ $$$$\mathrm{y}+\mathrm{z}=\mathrm{10}\:\wedge\:\mathrm{y},\mathrm{z}>\mathrm{0}\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{0}<\mathrm{y},\mathrm{z}<\mathrm{10}\Rightarrow\mathrm{y},\mathrm{z}\in\left(\mathrm{0},\mathrm{10}\right) \\ $$$$\mathrm{x}\in\left(\mathrm{0},\mathrm{6}\right)\: \\ $$$$\mathrm{y}\in\:\left(\mathrm{0},\mathrm{6}\right)\cap\left(\mathrm{0},\mathrm{10}\right)=\left(\mathrm{0},\mathrm{6}\right) \\ $$$$\mathrm{z}\in\left(\mathrm{4},\mathrm{10}\right) \\ $$$$\:\: \\ $$

Commented by Rasheed.Sindhi last updated on 16/Dec/18