Question Number 87464 by jagoll last updated on 04/Apr/20
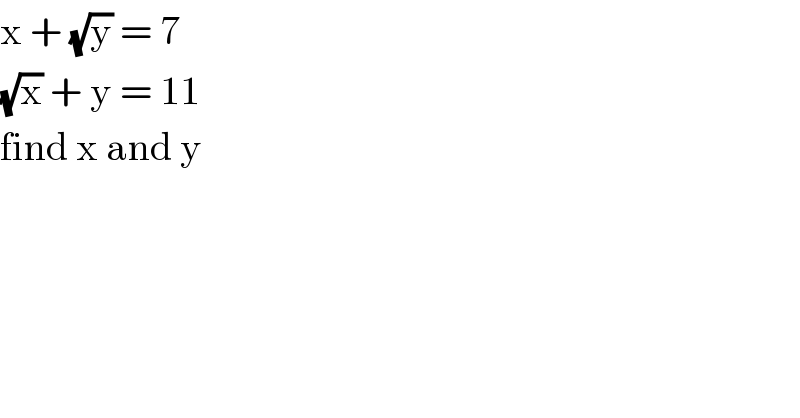
$$\mathrm{x}\:+\:\sqrt{\mathrm{y}}\:=\:\mathrm{7} \\ $$$$\sqrt{\mathrm{x}}\:+\:\mathrm{y}\:=\:\mathrm{11}\: \\ $$$$\mathrm{find}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}\: \\ $$
Commented by john santu last updated on 04/Apr/20

$$\mathrm{y}\:=\:\mathrm{9}\:\wedge\:\mathrm{x}\:=\:\mathrm{4} \\ $$
Commented by john santu last updated on 05/Apr/20
![(√y) = 7−x y = 49−14x+x^2 11−(√x) = 49 −14x + x^2 x^2 −14x+(√x) + 38 = 0 [ (√x) = w ] w^(4 ) −14w^2 +w + 38 = 0 (w−2)(w^3 +2w^2 −10w−19)=0 w = 2 = (√x) ⇒ x = 4 ⇒(√y) = 7−4 = 3 ⇒ y = 9](https://www.tinkutara.com/question/Q87470.png)
$$\sqrt{\mathrm{y}}\:=\:\mathrm{7}−\mathrm{x}\: \\ $$$$\mathrm{y}\:=\:\mathrm{49}−\mathrm{14x}+\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{11}−\sqrt{\mathrm{x}}\:=\:\mathrm{49}\:−\mathrm{14x}\:+\:\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{14x}+\sqrt{\mathrm{x}}\:+\:\mathrm{38}\:=\:\mathrm{0} \\ $$$$\left[\:\sqrt{\mathrm{x}}\:=\:\mathrm{w}\:\right] \\ $$$$\mathrm{w}^{\mathrm{4}\:} −\mathrm{14w}^{\mathrm{2}} +\mathrm{w}\:+\:\mathrm{38}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{w}−\mathrm{2}\right)\left(\mathrm{w}^{\mathrm{3}} +\mathrm{2w}^{\mathrm{2}} −\mathrm{10w}−\mathrm{19}\right)=\mathrm{0} \\ $$$$\mathrm{w}\:=\:\mathrm{2}\:=\:\sqrt{\mathrm{x}}\:\Rightarrow\:\mathrm{x}\:=\:\mathrm{4} \\ $$$$\Rightarrow\sqrt{\mathrm{y}}\:=\:\mathrm{7}−\mathrm{4}\:=\:\mathrm{3}\:\Rightarrow\:\mathrm{y}\:=\:\mathrm{9} \\ $$
