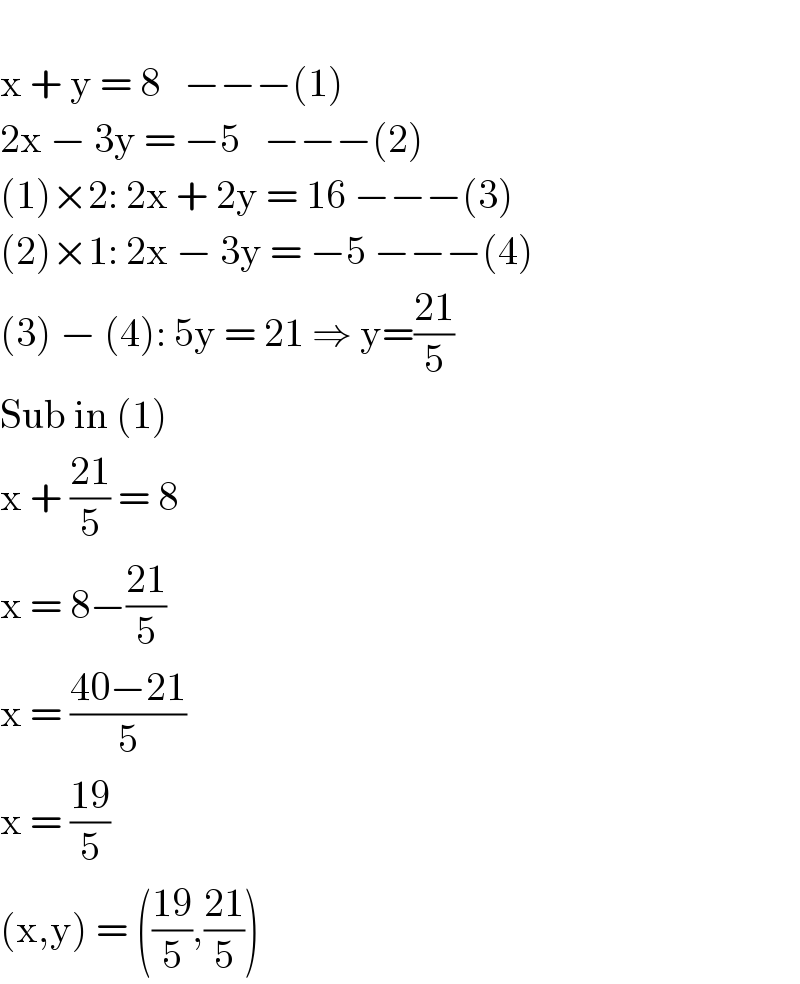Menu Close

x-y-8-2x-3y-5-the-number-8-is-wrong-i-solved-it-many-times-x-5-y-5-another-answers-x-7-5-y-13-5-please-help-

Tinku Tara 0 Comments
Pin




Question Number 123184 by solstis last updated on 23/Nov/20
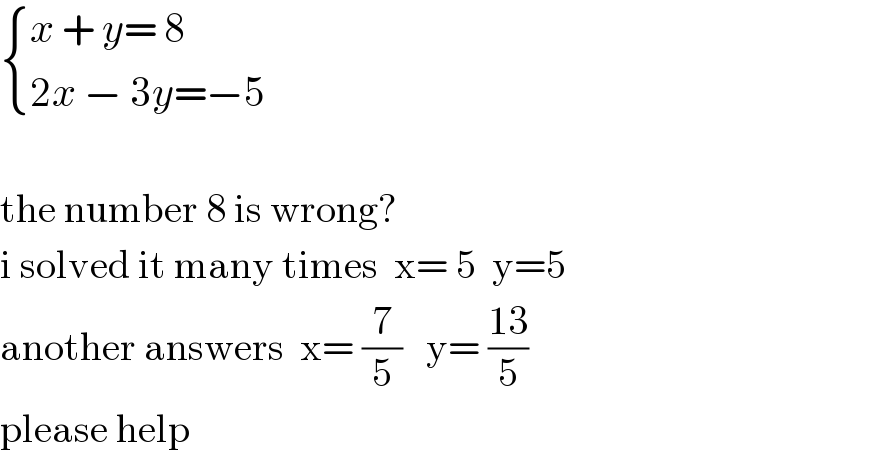
{ ((x + y= 8)),((2x − 3y=−5 )) :} the number 8 is wrong? i solved it many times x= 5 y=5 another answers x= (7/5) y= ((13)/5) please help
{x+y=82x−3y=−5thenumber8iswrong?isolveditmanytimesx=5y=5anotheranswersx=75y=135pleasehelp
Commented by MJS_new last updated on 23/Nov/20
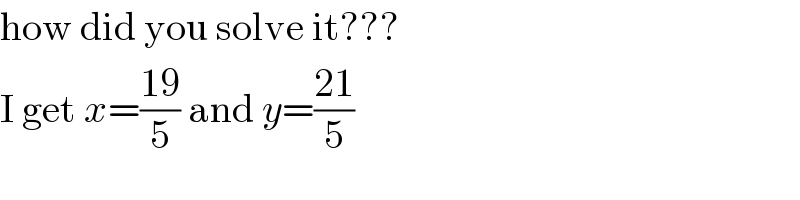
how did you solve it??? I get x=((19)/5) and y=((21)/5)
howdidyousolveit???Igetx=195andy=215
Commented by MJS_new last updated on 23/Nov/20
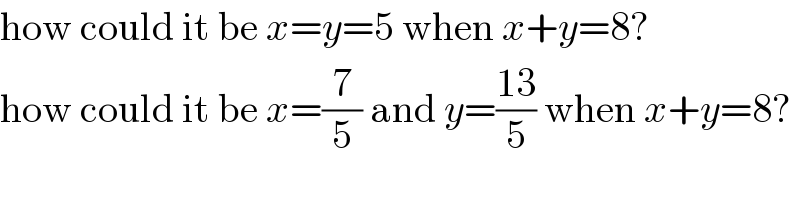
how could it be x=y=5 when x+y=8? how could it be x=(7/5) and y=((13)/5) when x+y=8?
howcoulditbex=y=5whenx+y=8?howcoulditbex=75andy=135whenx+y=8?
Commented by JDamian last updated on 23/Nov/20
Are you kidding? Your solutions are wrong but you question de data?!!
Commented by Lordose last updated on 23/Nov/20
That was what I wanted to ask It's kinda funny though
Commented by solstis last updated on 23/Nov/20
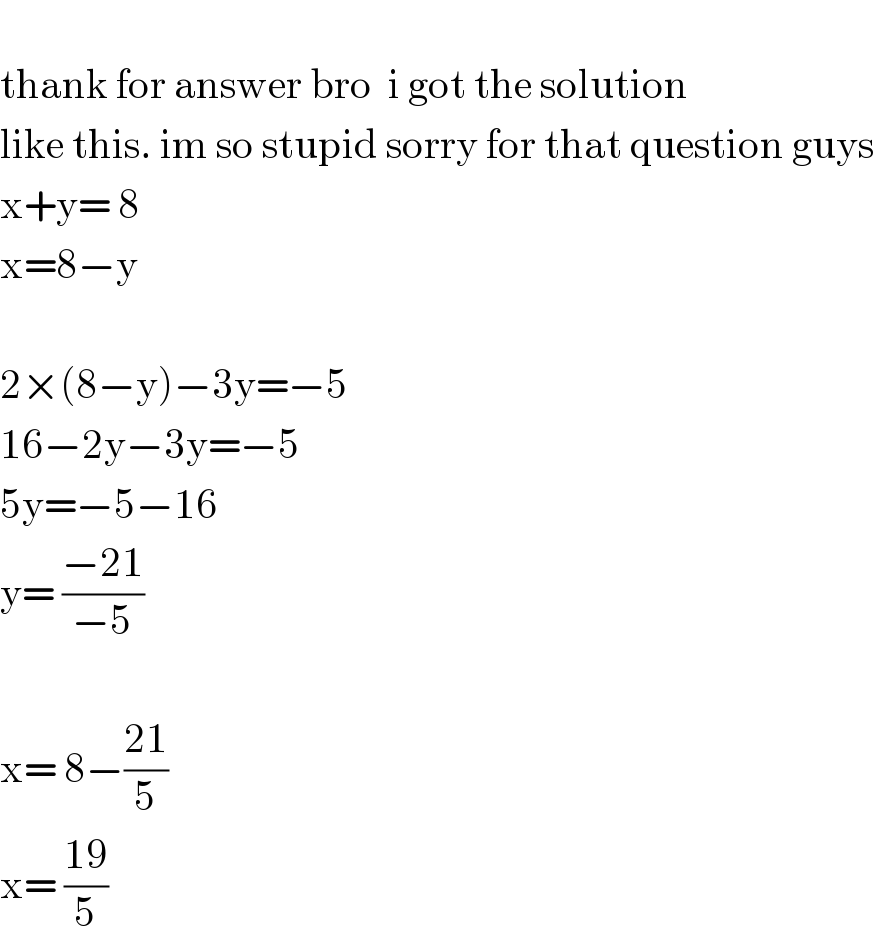
thank for answer bro i got the solution like this. im so stupid sorry for that question guys x+y= 8 x=8−y 2×(8−y)−3y=−5 16−2y−3y=−5 5y=−5−16 y= ((−21)/(−5)) x= 8−((21)/5) x= ((19)/5)
thankforanswerbroigotthesolutionlikethis.imsostupidsorryforthatquestionguysx+y=8x=8−y2×(8−y)−3y=−516−2y−3y=−55y=−5−16y=−21−5x=8−215x=195
Answered by Lordose last updated on 23/Nov/20
x + y = 8 −−−(1) 2x − 3y = −5 −−−(2) (1)×2: 2x + 2y = 16 −−−(3) (2)×1: 2x − 3y = −5 −−−(4) (3) − (4): 5y = 21 ⇒ y=((21)/5) Sub in (1) x + ((21)/5) = 8 x = 8−((21)/5) x = ((40−21)/5) x = ((19)/5) (x,y) = (((19)/5),((21)/5))
x+y=8−−−(1)2x−3y=−5−−−(2)(1)×2:2x+2y=16−−−(3)(2)×1:2x−3y=−5−−−(4)(3)−(4):5y=21⇒y=215Subin(1)x+215=8x=8−215x=40−215x=195(x,y)=(195,215)

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *