Question Number 54595 by ajfour last updated on 07/Feb/19

$$\:\:\:\:\:{x}+{y}={a} \\ $$$$\:\:\:\:\:{z}+{bx}={c} \\ $$$$\:\:\:\:\:{bz}+{xy}={d} \\ $$$$\:\:\:\:\:{Find}\:{yz}\:{in}\:{terms}\:{of}\:{a},{b},{c},{d}. \\ $$
Commented by mr W last updated on 07/Feb/19
![y=a−x z=c−bx b(c−bx)+x(a−x)=d x^2 +(b^2 −a)x+d−bc=0 x=((a−b^2 ±(√((b^2 −a)^2 −4(d−bc))))/2) yz=(a−x)(c−bx) ⇒yz=(([a+b^2 ±(√((b^2 −a)^2 −4(d−bc)))][2c+b^3 −ab±b(√((b^2 −a)^2 −4(d−bc)))])/4)](https://www.tinkutara.com/question/Q54601.png)
$${y}={a}−{x} \\ $$$${z}={c}−{bx} \\ $$$${b}\left({c}−{bx}\right)+{x}\left({a}−{x}\right)={d} \\ $$$${x}^{\mathrm{2}} +\left({b}^{\mathrm{2}} −{a}\right){x}+{d}−{bc}=\mathrm{0} \\ $$$${x}=\frac{{a}−{b}^{\mathrm{2}} \pm\sqrt{\left({b}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} −\mathrm{4}\left({d}−{bc}\right)}}{\mathrm{2}} \\ $$$${yz}=\left({a}−{x}\right)\left({c}−{bx}\right) \\ $$$$\Rightarrow{yz}=\frac{\left[{a}+{b}^{\mathrm{2}} \pm\sqrt{\left({b}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} −\mathrm{4}\left({d}−{bc}\right)}\right]\left[\mathrm{2}{c}+{b}^{\mathrm{3}} −{ab}\pm{b}\sqrt{\left({b}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} −\mathrm{4}\left({d}−{bc}\right)}\right]}{\mathrm{4}} \\ $$
Commented by ajfour last updated on 07/Feb/19
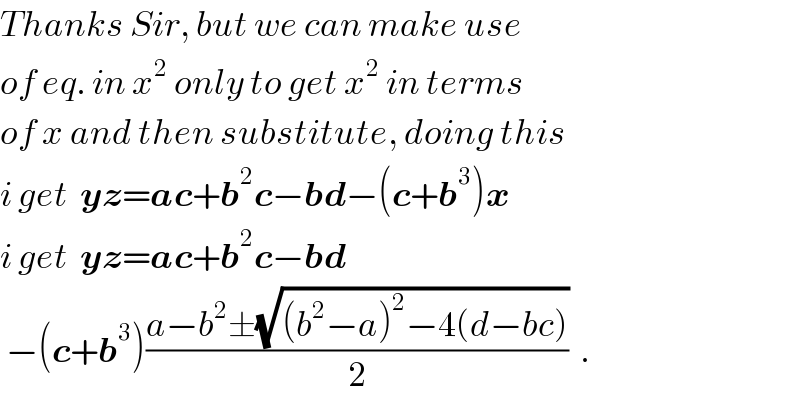
$${Thanks}\:{Sir},\:{but}\:{we}\:{can}\:{make}\:{use} \\ $$$${of}\:{eq}.\:{in}\:{x}^{\mathrm{2}} \:{only}\:{to}\:{get}\:{x}^{\mathrm{2}} \:{in}\:{terms} \\ $$$${of}\:{x}\:{and}\:{then}\:{substitute},\:{doing}\:{this} \\ $$$${i}\:{get}\:\:\boldsymbol{{yz}}=\boldsymbol{{ac}}+\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{c}}−\boldsymbol{{bd}}−\left(\boldsymbol{{c}}+\boldsymbol{{b}}^{\mathrm{3}} \right)\boldsymbol{{x}}\: \\ $$$${i}\:{get}\:\:\boldsymbol{{yz}}=\boldsymbol{{ac}}+\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{c}}−\boldsymbol{{bd}}\: \\ $$$$\:−\left(\boldsymbol{{c}}+\boldsymbol{{b}}^{\mathrm{3}} \right)\frac{{a}−{b}^{\mathrm{2}} \pm\sqrt{\left({b}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} −\mathrm{4}\left({d}−{bc}\right)}}{\mathrm{2}}\:\:. \\ $$
Commented by mr W last updated on 07/Feb/19

$${right}\:{sir}. \\ $$
