Question Number 92838 by i jagooll last updated on 09/May/20
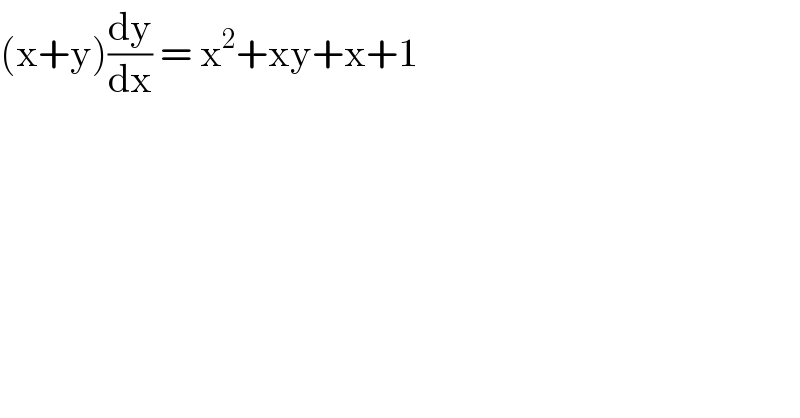
$$\left(\mathrm{x}+\mathrm{y}\right)\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{x}^{\mathrm{2}} +\mathrm{xy}+\mathrm{x}+\mathrm{1} \\ $$
Commented by john santu last updated on 09/May/20
![(x+y) (dy/dx) = x(x+y)+x+1 set x+y = v ⇒1+(dy/dx) = (dv/dx) (dy/dx) = (dv/dx) −1 ⇒v [ (dv/dx)−1] = xv +x+1 v (dv/dx) = v(x+1)+x+1 v (dv/dx) = (x+1)(v+1) ((v dv)/(v+1)) = (x+1) dx ∫ ((v+1−1)/(v+1)) dv = (1/2)(x+1)^2 +c v−ln (v+1) = (1/2)(x+1)^2 +c x+y−ln(x+y+1)=(1/2)(x+1)^2 +c y−ln(x+y+1)=(1/2)(x+1)^2 −x+c](https://www.tinkutara.com/question/Q92846.png)
$$\left(\mathrm{x}+\mathrm{y}\right)\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{x}\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{set}\:\mathrm{x}+\mathrm{y}\:=\:\mathrm{v}\:\Rightarrow\mathrm{1}+\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{dv}}{\mathrm{dx}}\:−\mathrm{1}\: \\ $$$$\Rightarrow\mathrm{v}\:\left[\:\frac{\mathrm{dv}}{\mathrm{dx}}−\mathrm{1}\right]\:=\:\mathrm{xv}\:+\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{v}\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\mathrm{v}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{v}\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{v}+\mathrm{1}\right) \\ $$$$\frac{\mathrm{v}\:\mathrm{dv}}{\mathrm{v}+\mathrm{1}}\:=\:\left(\mathrm{x}+\mathrm{1}\right)\:\mathrm{dx}\: \\ $$$$\int\:\frac{\mathrm{v}+\mathrm{1}−\mathrm{1}}{\mathrm{v}+\mathrm{1}}\:\mathrm{dv}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{c} \\ $$$$\mathrm{v}−\mathrm{ln}\:\left(\mathrm{v}+\mathrm{1}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{c} \\ $$$$\mathrm{x}+\mathrm{y}−\mathrm{ln}\left(\mathrm{x}+\mathrm{y}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{c}\: \\ $$$$\mathrm{y}−\mathrm{ln}\left(\mathrm{x}+\mathrm{y}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{x}+\mathrm{c}\: \\ $$
Commented by i jagooll last updated on 09/May/20
cool man sir ��
Commented by niroj last updated on 09/May/20
great dear����
Commented by john santu last updated on 09/May/20
ha ha ha ������
