Question Number 151496 by puissant last updated on 21/Aug/21
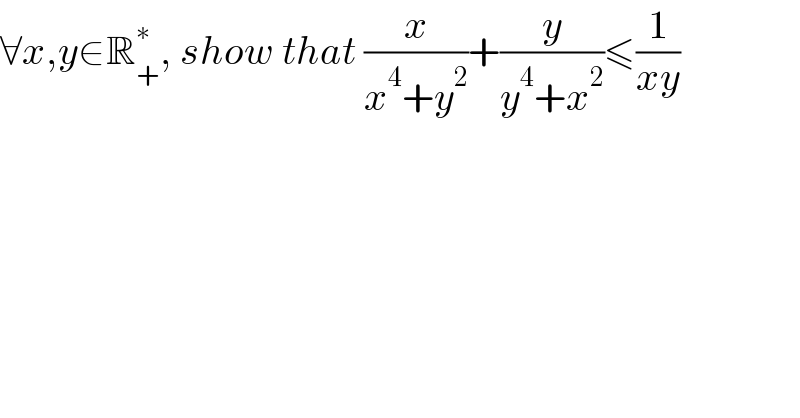
$$\forall{x},{y}\in\mathbb{R}_{+} ^{\ast} ,\:{show}\:{that}\:\frac{{x}}{{x}^{\mathrm{4}} +{y}^{\mathrm{2}} }+\frac{{y}}{{y}^{\mathrm{4}} +{x}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{{xy}} \\ $$
Answered by dumitrel last updated on 21/Aug/21
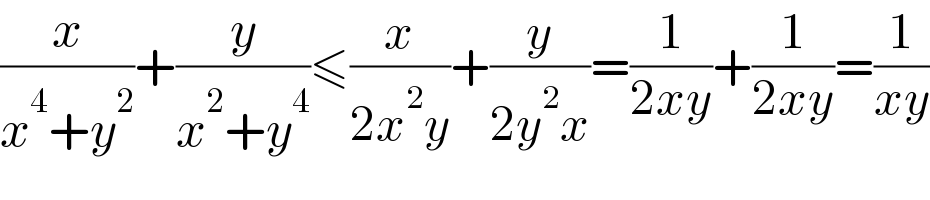
$$\frac{{x}}{{x}^{\mathrm{4}} +{y}^{\mathrm{2}} }+\frac{{y}}{{x}^{\mathrm{2}} +{y}^{\mathrm{4}} }\leqslant\frac{{x}}{\mathrm{2}{x}^{\mathrm{2}} {y}}+\frac{{y}}{\mathrm{2}{y}^{\mathrm{2}} {x}}=\frac{\mathrm{1}}{\mathrm{2}{xy}}+\frac{\mathrm{1}}{\mathrm{2}{xy}}=\frac{\mathrm{1}}{{xy}} \\ $$
