Question Number 104832 by bemath last updated on 24/Jul/20
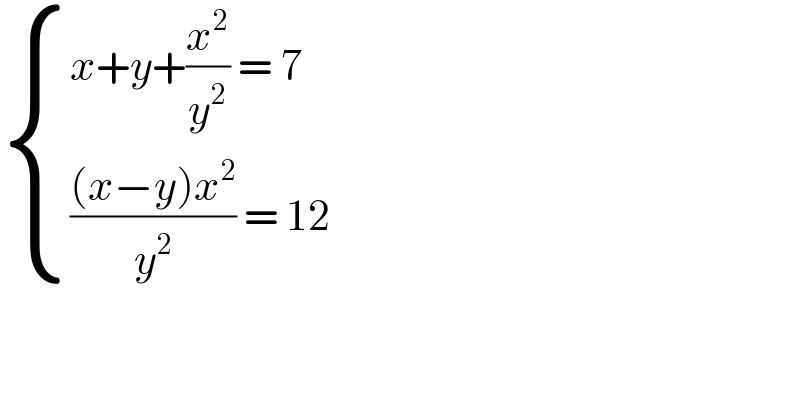
$$\begin{cases}{{x}+{y}+\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\:=\:\mathrm{7}}\\{\frac{\left({x}−{y}\right){x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\:=\:\mathrm{12}\:}\end{cases} \\ $$
Answered by john santu last updated on 24/Jul/20

$${let}\:{x}\:=\:\lambda{y}\:\rightarrow\begin{cases}{\lambda{y}+{y}+\frac{\lambda^{\mathrm{2}} {y}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\:=\:\mathrm{7}}\\{\frac{\left(\lambda{y}−{y}\right)\lambda^{\mathrm{2}} {y}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\:=\:\mathrm{12}}\end{cases} \\ $$$$\rightarrow\begin{cases}{\left(\lambda+\mathrm{1}\right){y}\:+\:\lambda^{\mathrm{2}} \:=\:\mathrm{7}}\\{\left(\lambda−\mathrm{1}\right)\lambda^{\mathrm{2}} {y}\:=\:\mathrm{12}}\end{cases} \\ $$$$\rightarrow\:\frac{\mathrm{7}−\lambda^{\mathrm{2}} }{\lambda+\mathrm{1}}\:=\:\frac{\mathrm{12}}{\lambda^{\mathrm{2}} \left(\lambda−\mathrm{1}\right)} \\ $$$$\left(\mathrm{7}−\lambda^{\mathrm{2}} \right)\lambda^{\mathrm{2}} \left(\lambda−\mathrm{1}\right)\:=\:\mathrm{12}\left(\lambda+\mathrm{1}\right) \\ $$$$\lambda^{\mathrm{5}} −\lambda^{\mathrm{4}} −\mathrm{7}\lambda^{\mathrm{3}} +\mathrm{7}\lambda^{\mathrm{2}} +\mathrm{12}\lambda+\mathrm{12}\:=\:\mathrm{0} \\ $$$${approximation} \\ $$$$\lambda\:=\:−\mathrm{2}.\mathrm{484293386} \\ $$$${y}\:=\:−\mathrm{0}.\mathrm{558034131} \\ $$$${then}\:{x}\:=\:\mathrm{1}.\mathrm{386320501} \\ $$
