Menu Close

x-y-x-95-8-y-x-y-93-8-Find-xy-

Tinku Tara 0 Comments
Pin




Question Number 107313 by bemath last updated on 10/Aug/20
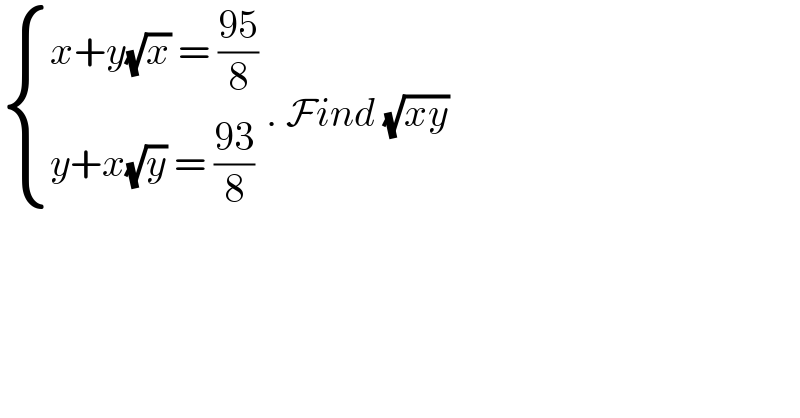
{ ((x+y(√x) = ((95)/8))),((y+x(√y) = ((93)/8))) :} . Find (√(xy))
$$\begin{cases}{{x}+{y}\sqrt{{x}}\:=\:\frac{\mathrm{95}}{\mathrm{8}}}\\{{y}+{x}\sqrt{{y}}\:=\:\frac{\mathrm{93}}{\mathrm{8}}}\end{cases}\:.\:\mathcal{F}{ind}\:\sqrt{{xy}} \\ $$
Answered by Her_Majesty last updated on 10/Aug/20
answered qu 106259
$${answered} \\ $$$${qu}\:\mathrm{106259} \\ $$
Answered by 1549442205PVT last updated on 26/Aug/20
Set (√x)+(√y)=a,(√(xy)) =b we have ((√x)−(√y))^2 =((√x)+(√y))^2 −4(√(xy))=a^2 −4b ⇒(√x)+(√y)=(√(a^2 −4b)). From that we get { (((√x)=((a+(√(a^2 −4b)))/2))),(((√y)=((a−(√(a^2 −4b)))/2))) :} ⇒ { ((x=((a^2 −2b+a(√(a^2 −4b)))/2))),((y=((a^2 −2b−a(√(a^2 −4b)))/2))) :} (∗) Substracting two equations we get x−y+(√(xy))((√y)−(√x))=(1/4) ⇔a(√(a^2 −4b)) −b(√(a^2 −4b)) =(1/4) ⇔(a−b)(√(a^2 −4b)) =(1/4) ⇔(a^2 −2ab+b^2 )(a^2 −4b)=(1/(16))(1) Adding up two equations we get x+y+(√(xy)) ((√x) +(√y) )=((47)/2) ⇔a^2 −2b+ab=((47)/2)⇒b=((2a^2 −47)/(4−2a))(2) ⇒b^2 =((4a^4 −188a^2 +2209)/(4a^2 −16a+16)).Replace into (1)we get [(a^2 −((4a^3 −94a)/(4−2a))+((4a^4 −188a^2 +2209)/(4a^2 −16a+16)).)(a^2 −((8a^2 −188)/(4−2a)))=(1/(16)) ⇒((4a^4 −16a^3 +16a^2 +8a^4 −16a^3 −188a^2 +376a+4a^4 −188a^2 +2209)/(4a^4 −16a+16))×((2a^3 +4a^2 −188)/(2a−4))=(1/(16)) After simple transformations we get 64a^7 −1696a^5 −7392a^4 +23875a^3 +153038a^2 −141376a−830576=0 ⇔(a−4)(64a^6 +256a^5 −672a^4 −10080a^3 −16445a^2 +87258a+207644)=0 ⇒a−4=0⇔a=4 We shall prove that the equation 64a^6 +256a^5 −672a^4 −10080a^3 −16445a^2 +87258a+207644=0 has no positive roots^((•)) (leave later) Replace into(2)we obtain b=((15)/4) substituting into (∗) we get x=((a^2 −2b+a(√(4a^2 −b)))/2)=((25)/4), y=((a^2 −2b−a(√(4a^2 −b)))/2)=(9/9) Thus,(√(xy))=b=15/4 Now we need have to prove that the eqn. 64x^6 +256x^5 −672x^4 −10080x^3 −17445x^2 +87258x+207644=0 has no positive roots Put x=(1/u) then our problem reduce to Prove that the equation 207644t^6 +87258t^5 −16445t^4 −10080t^3 −672t^2 +256t+64=0 has no positive roots .Indeed, Apply Cauchy′s inequality for positive numbers we have 64000t^6 +64000t^5 +64t≥3^3 (√(64^3 ×10^6 t^(12) ))=19200t^4 Hence,LHS≥143644t^6 +23258t^5 +2755t^4 −10080t^3 −672t^2 +192t+64 We have also 23258t^5 +2755t^4 ≥(√(23258.2755t))
$$\:\mathrm{Set}\:\sqrt{\mathrm{x}}+\sqrt{\mathrm{y}}=\mathrm{a},\sqrt{\mathrm{xy}}\:=\mathrm{b}\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(\sqrt{\mathrm{x}}−\sqrt{\mathrm{y}}\right)^{\mathrm{2}} =\left(\sqrt{\mathrm{x}}+\sqrt{\mathrm{y}}\right)^{\mathrm{2}} −\mathrm{4}\sqrt{\mathrm{xy}}=\mathrm{a}^{\mathrm{2}} −\mathrm{4b} \\ $$$$\Rightarrow\sqrt{\mathrm{x}}+\sqrt{\mathrm{y}}=\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{4b}}.\:\mathrm{From}\:\mathrm{that}\:\mathrm{we}\:\mathrm{get} \\ $$$$\begin{cases}{\sqrt{\mathrm{x}}=\frac{\mathrm{a}+\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{4b}}}{\mathrm{2}}}\\{\sqrt{\mathrm{y}}=\frac{\mathrm{a}−\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{4b}}}{\mathrm{2}}}\end{cases}\:\Rightarrow\begin{cases}{\mathrm{x}=\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{2b}+\mathrm{a}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{4b}}}{\mathrm{2}}}\\{\mathrm{y}=\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{2b}−\mathrm{a}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{4b}}}{\mathrm{2}}}\end{cases}\:\left(\ast\right) \\ $$$$\mathrm{Substracting}\:\mathrm{two}\:\mathrm{equations}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}−\mathrm{y}+\sqrt{\mathrm{xy}}\left(\sqrt{\mathrm{y}}−\sqrt{\mathrm{x}}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Leftrightarrow\mathrm{a}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{4b}}\:−\mathrm{b}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{4b}}\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Leftrightarrow\left(\mathrm{a}−\mathrm{b}\right)\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{4b}}\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Leftrightarrow\left(\mathrm{a}^{\mathrm{2}} −\mathrm{2ab}+\mathrm{b}^{\mathrm{2}} \right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{4b}\right)=\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{1}\right) \\ $$$$\mathrm{Adding}\:\mathrm{up}\:\mathrm{two}\:\mathrm{equations}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}+\mathrm{y}+\sqrt{\mathrm{xy}}\:\left(\sqrt{\mathrm{x}}\:+\sqrt{\mathrm{y}}\:\right)=\frac{\mathrm{47}}{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{a}^{\mathrm{2}} −\mathrm{2b}+\mathrm{ab}=\frac{\mathrm{47}}{\mathrm{2}}\Rightarrow\mathrm{b}=\frac{\mathrm{2a}^{\mathrm{2}} −\mathrm{47}}{\mathrm{4}−\mathrm{2a}}\left(\mathrm{2}\right) \\ $$$$\Rightarrow\mathrm{b}^{\mathrm{2}} =\frac{\mathrm{4a}^{\mathrm{4}} −\mathrm{188a}^{\mathrm{2}} +\mathrm{2209}}{\mathrm{4a}^{\mathrm{2}} −\mathrm{16a}+\mathrm{16}}.\mathrm{Replace}\:\mathrm{into} \\ $$$$\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\left[\left(\mathrm{a}^{\mathrm{2}} −\frac{\mathrm{4a}^{\mathrm{3}} −\mathrm{94a}}{\mathrm{4}−\mathrm{2a}}+\frac{\mathrm{4a}^{\mathrm{4}} −\mathrm{188a}^{\mathrm{2}} +\mathrm{2209}}{\mathrm{4a}^{\mathrm{2}} −\mathrm{16a}+\mathrm{16}}.\right)\left(\mathrm{a}^{\mathrm{2}} −\frac{\mathrm{8a}^{\mathrm{2}} −\mathrm{188}}{\mathrm{4}−\mathrm{2a}}\right)=\frac{\mathrm{1}}{\mathrm{16}}\right. \\ $$$$\Rightarrow\frac{\mathrm{4a}^{\mathrm{4}} −\mathrm{16a}^{\mathrm{3}} +\mathrm{16a}^{\mathrm{2}} +\mathrm{8a}^{\mathrm{4}} −\mathrm{16a}^{\mathrm{3}} −\mathrm{188a}^{\mathrm{2}} +\mathrm{376a}+\mathrm{4a}^{\mathrm{4}} −\mathrm{188a}^{\mathrm{2}} +\mathrm{2209}}{\mathrm{4a}^{\mathrm{4}} −\mathrm{16a}+\mathrm{16}}×\frac{\mathrm{2a}^{\mathrm{3}} +\mathrm{4a}^{\mathrm{2}} −\mathrm{188}}{\mathrm{2a}−\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\mathrm{After}\:\mathrm{simple}\:\mathrm{transformations}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{64a}^{\mathrm{7}} −\mathrm{1696a}^{\mathrm{5}} −\mathrm{7392a}^{\mathrm{4}} +\mathrm{23875a}^{\mathrm{3}} +\mathrm{153038a}^{\mathrm{2}} −\mathrm{141376a}−\mathrm{830576}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{a}−\mathrm{4}\right)\left(\mathrm{64a}^{\mathrm{6}} +\mathrm{256a}^{\mathrm{5}} −\mathrm{672a}^{\mathrm{4}} −\mathrm{10080a}^{\mathrm{3}} −\mathrm{16445a}^{\mathrm{2}} +\mathrm{87258a}+\mathrm{207644}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{a}−\mathrm{4}=\mathrm{0}\Leftrightarrow\mathrm{a}=\mathrm{4} \\ $$$$\mathrm{We}\:\mathrm{shall}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{64a}^{\mathrm{6}} +\mathrm{256a}^{\mathrm{5}} −\mathrm{672a}^{\mathrm{4}} −\mathrm{10080a}^{\mathrm{3}} −\mathrm{16445a}^{\mathrm{2}} +\mathrm{87258a}+\mathrm{207644}=\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{no}\:\mathrm{positive}\:\mathrm{roots}\:^{\left(\bullet\right)} \left(\mathrm{leave}\:\mathrm{later}\right) \\ $$$$\mathrm{Replace}\:\mathrm{into}\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{obtain}\:\mathrm{b}=\frac{\mathrm{15}}{\mathrm{4}} \\ $$$$\mathrm{substituting}\:\mathrm{into}\:\left(\ast\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}=\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{2b}+\mathrm{a}\sqrt{\mathrm{4a}^{\mathrm{2}} −\mathrm{b}}}{\mathrm{2}}=\frac{\mathrm{25}}{\mathrm{4}}, \\ $$$$\mathrm{y}=\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{2b}−\mathrm{a}\sqrt{\mathrm{4a}^{\mathrm{2}} −\mathrm{b}}}{\mathrm{2}}=\frac{\mathrm{9}}{\mathrm{9}} \\ $$$$\mathrm{Thus},\sqrt{\mathrm{xy}}=\mathrm{b}=\mathrm{15}/\mathrm{4} \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{need}\:\mathrm{have}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{eqn}. \\ $$$$\mathrm{64x}^{\mathrm{6}} +\mathrm{256x}^{\mathrm{5}} −\mathrm{672x}^{\mathrm{4}} −\mathrm{10080x}^{\mathrm{3}} −\mathrm{17445x}^{\mathrm{2}} +\mathrm{87258x}+\mathrm{207644}=\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{no}\:\mathrm{positive}\:\mathrm{roots} \\ $$$$\mathrm{Put}\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{u}}\:\mathrm{then}\:\mathrm{our}\:\mathrm{problem}\:\mathrm{reduce}\:\mathrm{to} \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{207644t}^{\mathrm{6}} +\mathrm{87258t}^{\mathrm{5}} −\mathrm{16445t}^{\mathrm{4}} −\mathrm{10080t}^{\mathrm{3}} \\ $$$$−\mathrm{672t}^{\mathrm{2}} +\mathrm{256t}+\mathrm{64}=\mathrm{0}\:\mathrm{has}\:\mathrm{no}\:\mathrm{positive}\:\mathrm{roots} \\ $$$$.\mathrm{Indeed}, \\ $$$$\mathrm{Apply}\:\mathrm{Cauchy}'\mathrm{s}\:\mathrm{inequality}\:\mathrm{for} \\ $$$$\mathrm{positive}\:\mathrm{numbers}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{64000t}^{\mathrm{6}} +\mathrm{64000t}^{\mathrm{5}} +\mathrm{64t}\geqslant\mathrm{3}\:^{\mathrm{3}} \sqrt{\mathrm{64}^{\mathrm{3}} ×\mathrm{10}^{\mathrm{6}} \mathrm{t}^{\mathrm{12}} }=\mathrm{19200t}^{\mathrm{4}} \\ $$$$\mathrm{Hence},\mathrm{LHS}\geqslant\mathrm{143644t}^{\mathrm{6}} +\mathrm{23258t}^{\mathrm{5}} +\mathrm{2755t}^{\mathrm{4}} \\ $$$$−\mathrm{10080t}^{\mathrm{3}} −\mathrm{672t}^{\mathrm{2}} +\mathrm{192t}+\mathrm{64} \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{also} \\ $$$$\mathrm{23258t}^{\mathrm{5}} +\mathrm{2755t}^{\mathrm{4}} \geqslant\sqrt{\mathrm{23258}.\mathrm{2755t}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *