Menu Close

x-y-xyz-1-4-y-z-xyz-1-24-x-z-xyz-1-24-

Tinku Tara 0 Comments
Pin




Question Number 160677 by tounghoungko last updated on 04/Dec/21
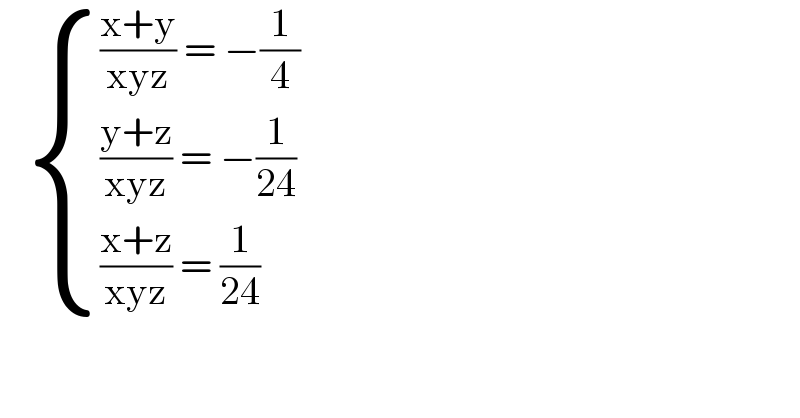
{ ((((x+y)/(xyz)) = −(1/4))),((((y+z)/(xyz)) = −(1/(24)))),((((x+z)/(xyz)) = (1/(24)))) :}
$$\:\:\:\begin{cases}{\frac{\mathrm{x}+\mathrm{y}}{\mathrm{xyz}}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}}\\{\frac{\mathrm{y}+\mathrm{z}}{\mathrm{xyz}}\:=\:−\frac{\mathrm{1}}{\mathrm{24}}}\\{\frac{\mathrm{x}+\mathrm{z}}{\mathrm{xyz}}\:=\:\frac{\mathrm{1}}{\mathrm{24}}}\end{cases}\: \\ $$$$\:\: \\ $$
Commented by bobhans last updated on 04/Dec/21
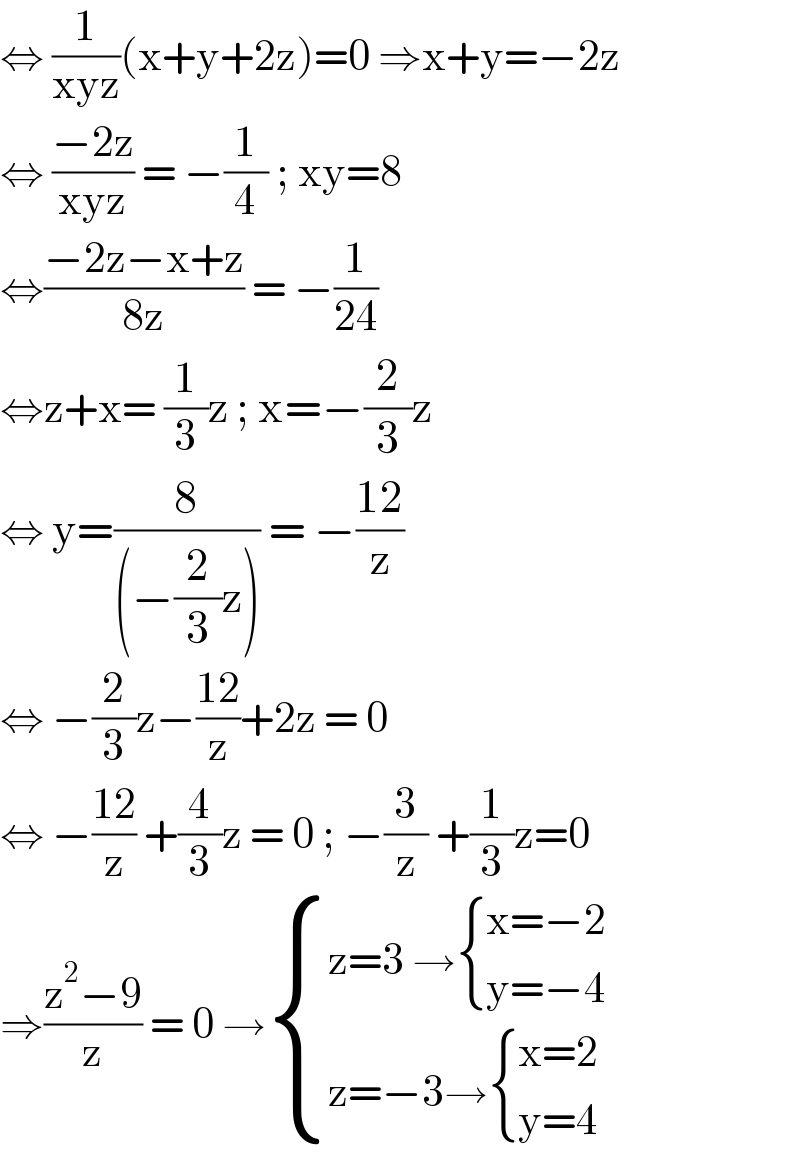
⇔ (1/(xyz))(x+y+2z)=0 ⇒x+y=−2z ⇔ ((−2z)/(xyz)) = −(1/4) ; xy=8 ⇔((−2z−x+z)/(8z)) = −(1/(24)) ⇔z+x= (1/3)z ; x=−(2/3)z ⇔ y=(8/((−(2/3)z))) = −((12)/z) ⇔ −(2/3)z−((12)/z)+2z = 0 ⇔ −((12)/z) +(4/3)z = 0 ; −(3/z) +(1/3)z=0 ⇒((z^2 −9)/z) = 0 → { ((z=3 → { ((x=−2)),((y=−4)) :})),((z=−3→ { ((x=2)),((y=4)) :})) :}
$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{xyz}}\left(\mathrm{x}+\mathrm{y}+\mathrm{2z}\right)=\mathrm{0}\:\Rightarrow\mathrm{x}+\mathrm{y}=−\mathrm{2z} \\ $$$$\Leftrightarrow\:\frac{−\mathrm{2z}}{\mathrm{xyz}}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\:;\:\mathrm{xy}=\mathrm{8} \\ $$$$\Leftrightarrow\frac{−\mathrm{2z}−\mathrm{x}+\mathrm{z}}{\mathrm{8z}}\:=\:−\frac{\mathrm{1}}{\mathrm{24}} \\ $$$$\Leftrightarrow\mathrm{z}+\mathrm{x}=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{z}\:;\:\mathrm{x}=−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{z} \\ $$$$\Leftrightarrow\:\mathrm{y}=\frac{\mathrm{8}}{\left(−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{z}\right)}\:=\:−\frac{\mathrm{12}}{\mathrm{z}} \\ $$$$\Leftrightarrow\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{z}−\frac{\mathrm{12}}{\mathrm{z}}+\mathrm{2z}\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:−\frac{\mathrm{12}}{\mathrm{z}}\:+\frac{\mathrm{4}}{\mathrm{3}}\mathrm{z}\:=\:\mathrm{0}\:;\:−\frac{\mathrm{3}}{\mathrm{z}}\:+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{z}=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{9}}{\mathrm{z}}\:=\:\mathrm{0}\:\rightarrow\begin{cases}{\mathrm{z}=\mathrm{3}\:\rightarrow\begin{cases}{\mathrm{x}=−\mathrm{2}}\\{\mathrm{y}=−\mathrm{4}}\end{cases}}\\{\mathrm{z}=−\mathrm{3}\rightarrow\begin{cases}{\mathrm{x}=\mathrm{2}}\\{\mathrm{y}=\mathrm{4}}\end{cases}}\end{cases} \\ $$
Answered by mahdipoor last updated on 04/Dec/21
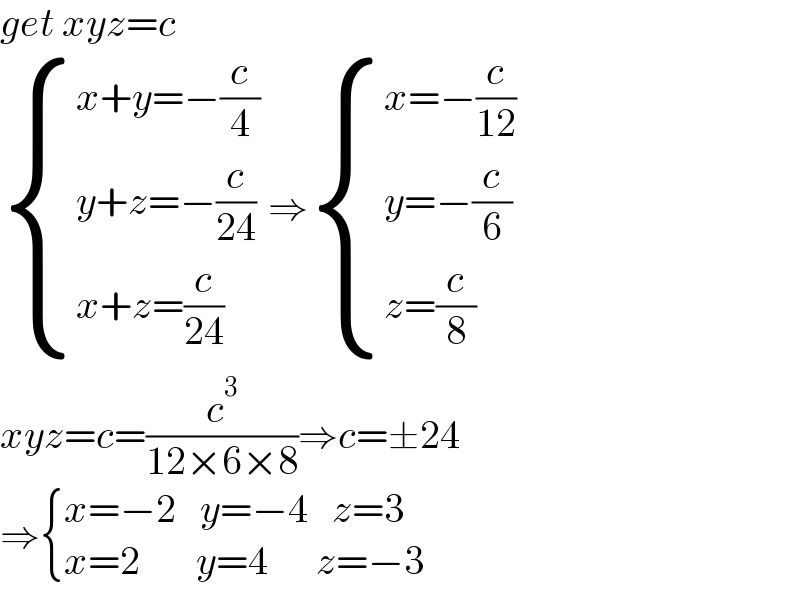
get xyz=c { ((x+y=−(c/4))),((y+z=−(c/(24)))),((x+z=(c/(24)))) :} ⇒ { ((x=−(c/(12)))),((y=−(c/6))),((z=(c/8))) :} xyz=c=(c^3 /(12×6×8))⇒c=±24 ⇒ { ((x=−2 y=−4 z=3)),((x=2 y=4 z=−3)) :}
$${get}\:{xyz}={c} \\ $$$$\begin{cases}{{x}+{y}=−\frac{{c}}{\mathrm{4}}}\\{{y}+{z}=−\frac{{c}}{\mathrm{24}}}\\{{x}+{z}=\frac{{c}}{\mathrm{24}}}\end{cases}\:\Rightarrow\begin{cases}{{x}=−\frac{{c}}{\mathrm{12}}}\\{{y}=−\frac{{c}}{\mathrm{6}}}\\{{z}=\frac{{c}}{\mathrm{8}}}\end{cases} \\ $$$${xyz}={c}=\frac{{c}^{\mathrm{3}} }{\mathrm{12}×\mathrm{6}×\mathrm{8}}\Rightarrow{c}=\pm\mathrm{24} \\ $$$$\Rightarrow\begin{cases}{{x}=−\mathrm{2}\:\:\:{y}=−\mathrm{4}\:\:\:{z}=\mathrm{3}}\\{{x}=\mathrm{2}\:\:\:\:\:\:\:{y}=\mathrm{4}\:\:\:\:\:\:{z}=−\mathrm{3}}\end{cases} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *