Question Number 117228 by bemath last updated on 10/Oct/20
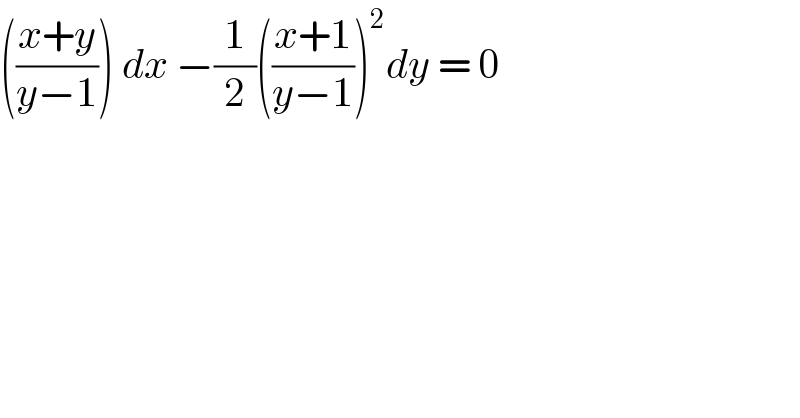
$$\left(\frac{{x}+{y}}{{y}−\mathrm{1}}\right)\:{dx}\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}+\mathrm{1}}{{y}−\mathrm{1}}\right)^{\mathrm{2}} {dy}\:=\:\mathrm{0} \\ $$
Answered by TANMAY PANACEA last updated on 10/Oct/20
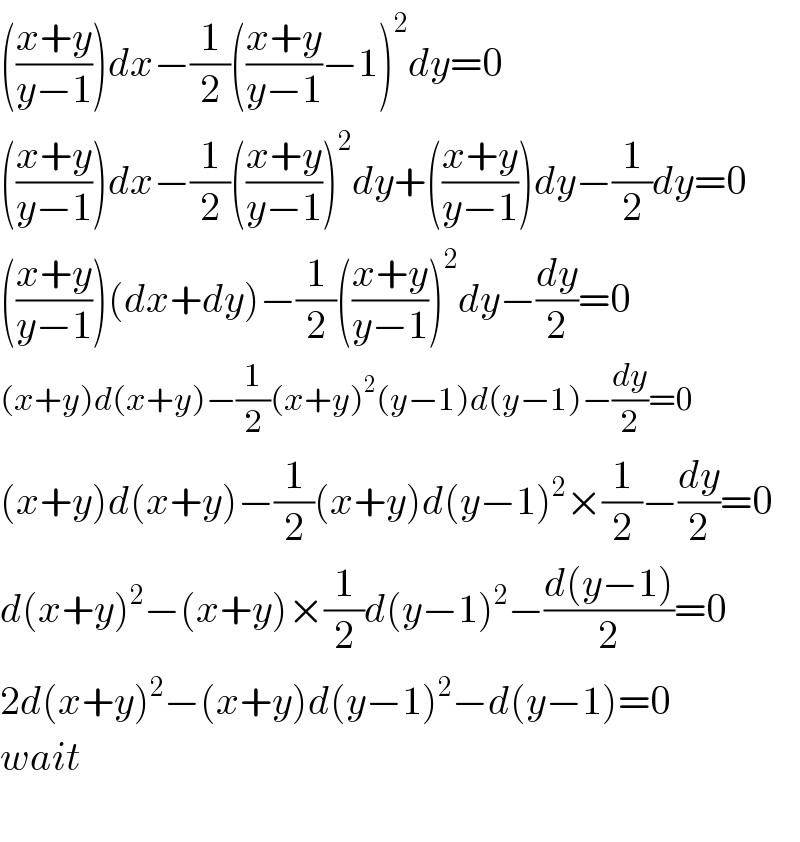
$$\left(\frac{{x}+{y}}{{y}−\mathrm{1}}\right){dx}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}+{y}}{{y}−\mathrm{1}}−\mathrm{1}\right)^{\mathrm{2}} {dy}=\mathrm{0} \\ $$$$\left(\frac{{x}+{y}}{{y}−\mathrm{1}}\right){dx}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}+{y}}{{y}−\mathrm{1}}\right)^{\mathrm{2}} {dy}+\left(\frac{{x}+{y}}{{y}−\mathrm{1}}\right){dy}−\frac{\mathrm{1}}{\mathrm{2}}{dy}=\mathrm{0} \\ $$$$\left(\frac{{x}+{y}}{{y}−\mathrm{1}}\right)\left({dx}+{dy}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}+{y}}{{y}−\mathrm{1}}\right)^{\mathrm{2}} {dy}−\frac{{dy}}{\mathrm{2}}=\mathrm{0} \\ $$$$\left({x}+{y}\right){d}\left({x}+{y}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left({x}+{y}\right)^{\mathrm{2}} \left({y}−\mathrm{1}\right){d}\left({y}−\mathrm{1}\right)−\frac{{dy}}{\mathrm{2}}=\mathrm{0} \\ $$$$\left({x}+{y}\right){d}\left({x}+{y}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left({x}+{y}\right){d}\left({y}−\mathrm{1}\right)^{\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{2}}−\frac{{dy}}{\mathrm{2}}=\mathrm{0} \\ $$$${d}\left({x}+{y}\right)^{\mathrm{2}} −\left({x}+{y}\right)×\frac{\mathrm{1}}{\mathrm{2}}{d}\left({y}−\mathrm{1}\right)^{\mathrm{2}} −\frac{{d}\left({y}−\mathrm{1}\right)}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{2}{d}\left({x}+{y}\right)^{\mathrm{2}} −\left({x}+{y}\right){d}\left({y}−\mathrm{1}\right)^{\mathrm{2}} −{d}\left({y}−\mathrm{1}\right)=\mathrm{0} \\ $$$${wait} \\ $$$$ \\ $$
