Question Number 102515 by bemath last updated on 09/Jul/20
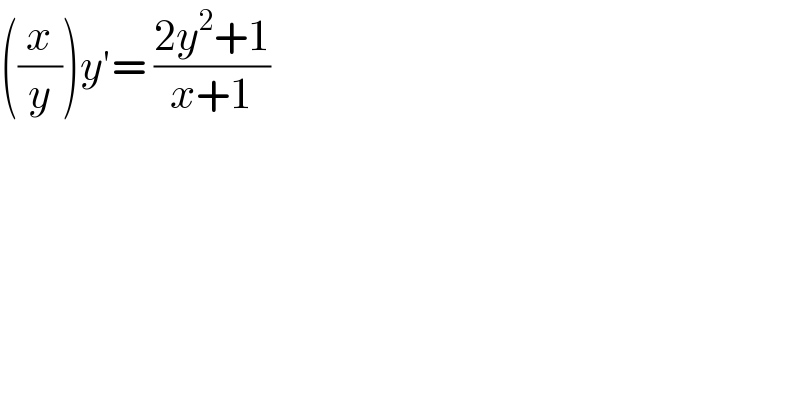
$$\left(\frac{{x}}{{y}}\right){y}'=\:\frac{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}}{{x}+\mathrm{1}} \\ $$
Answered by bobhans last updated on 09/Jul/20
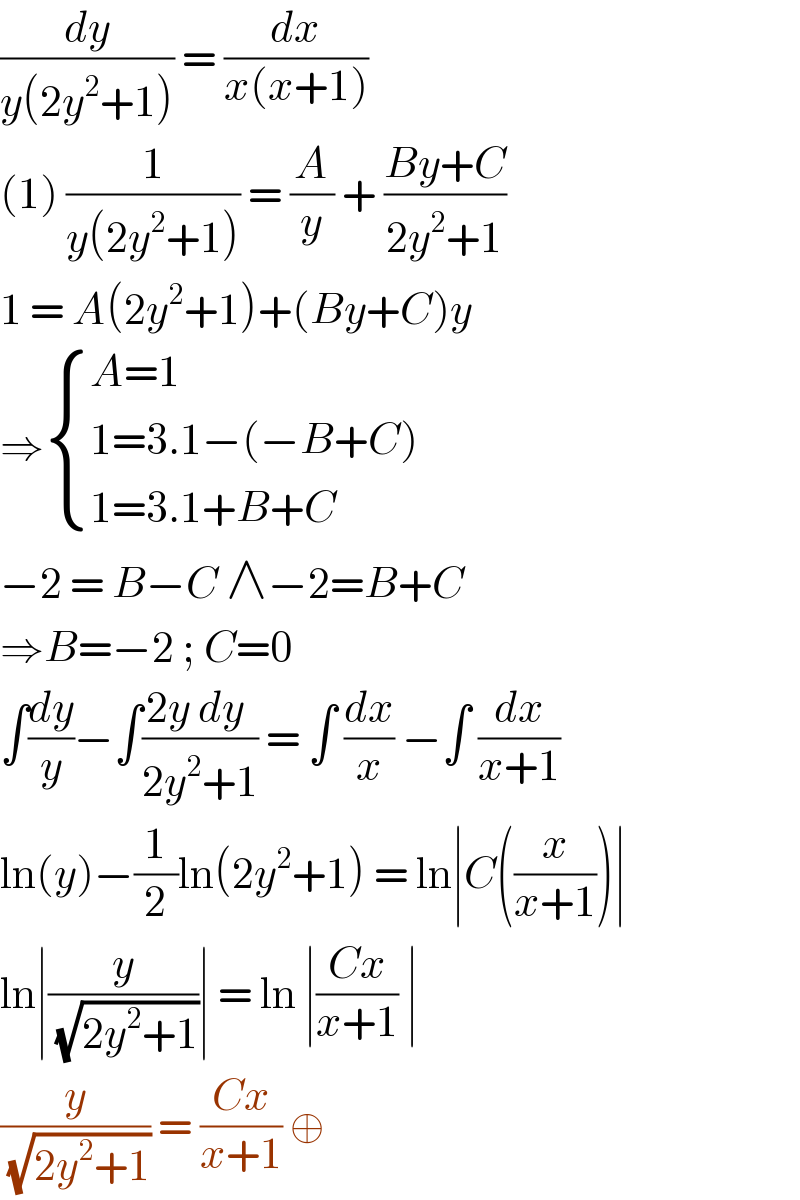
$$\frac{{dy}}{{y}\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}\right)}\:=\:\frac{{dx}}{{x}\left({x}+\mathrm{1}\right)} \\ $$$$\left(\mathrm{1}\right)\:\frac{\mathrm{1}}{{y}\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}\right)}\:=\:\frac{{A}}{{y}}\:+\:\frac{{By}+{C}}{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{1}\:=\:{A}\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}\right)+\left({By}+{C}\right){y}\: \\ $$$$\Rightarrow\begin{cases}{{A}=\mathrm{1}}\\{\mathrm{1}=\mathrm{3}.\mathrm{1}−\left(−{B}+{C}\right)}\\{\mathrm{1}=\mathrm{3}.\mathrm{1}+{B}+{C}}\end{cases} \\ $$$$−\mathrm{2}\:=\:{B}−{C}\:\wedge−\mathrm{2}={B}+{C} \\ $$$$\Rightarrow{B}=−\mathrm{2}\:;\:{C}=\mathrm{0} \\ $$$$\int\frac{{dy}}{{y}}−\int\frac{\mathrm{2}{y}\:{dy}\:}{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}}\:=\:\int\:\frac{{dx}}{{x}}\:−\int\:\frac{{dx}}{{x}+\mathrm{1}} \\ $$$$\mathrm{ln}\left({y}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}\right)\:=\:\mathrm{ln}\mid{C}\left(\frac{{x}}{{x}+\mathrm{1}}\right)\mid\: \\ $$$$\mathrm{ln}\mid\frac{{y}}{\:\sqrt{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}}}\mid\:=\:\mathrm{ln}\:\mid\frac{{Cx}}{{x}+\mathrm{1}}\:\mid\: \\ $$$$\frac{{y}}{\:\sqrt{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}}}\:=\:\frac{{Cx}}{{x}+\mathrm{1}}\:\oplus\: \\ $$
Answered by petrochengula last updated on 09/Jul/20

$$\frac{{dy}}{{y}\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{{dx}}{{x}\left({x}+\mathrm{1}\right)} \\ $$$${integrate}\:{both}\:{sides} \\ $$$$\int\frac{{dy}}{{y}^{\mathrm{3}} \left(\mathrm{2}+\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\right)}=\int\frac{{dx}}{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}}{{y}^{\mathrm{2}} }\right)={ln}\mid\frac{{Cx}}{\mathrm{1}+{x}}\mid+ \\ $$$${ln}\sqrt{\frac{{y}^{\mathrm{2}} }{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}}}={ln}\mid\frac{{Cx}}{\mathrm{1}+{x}}\mid \\ $$$$\frac{{y}}{\:\sqrt{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}}}=\frac{{Cx}}{\mathrm{1}+{x}} \\ $$
