Question Number 109738 by Khalmohmmad last updated on 25/Aug/20
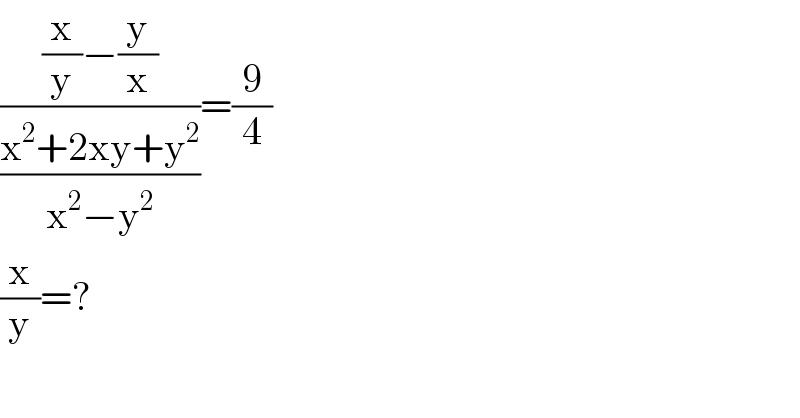
$$\frac{\frac{\mathrm{x}}{\mathrm{y}}−\frac{\mathrm{y}}{\mathrm{x}}}{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}=? \\ $$
Commented by nimnim last updated on 25/Aug/20

$$\mathrm{Sol}:\:\frac{\frac{\mathrm{x}}{\mathrm{y}}−\frac{\mathrm{y}}{\mathrm{x}}}{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\Rightarrow\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\mathrm{xy}}×\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} }=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\Rightarrow\frac{\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} }{\mathrm{xy}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\Rightarrow\frac{\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} }{\mathrm{4xy}}=\frac{\mathrm{9}}{\mathrm{16}}………\left(\mathrm{i}\right) \\ $$$$\Rightarrow\frac{\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} +\mathrm{4xy}}{\mathrm{4xy}}=\frac{\mathrm{9}+\mathrm{16}}{\mathrm{16}}\:\:\left\{\mathrm{componendo}\right\} \\ $$$$\Rightarrow\frac{\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} }{\mathrm{4xy}}=\frac{\mathrm{25}}{\mathrm{16}}……..\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{ii}\right)\boldsymbol{\div}\left(\mathrm{i}\right)\Rightarrow\frac{\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} }{\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} }=\frac{\mathrm{25}}{\mathrm{9}} \\ $$$$\Rightarrow\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}=\frac{\mathrm{5}}{\mathrm{3}}\:\:\mathrm{or}\:\:\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}=−\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{by}\:\mathrm{componendo}\:\mathrm{and}\:\mathrm{dividendo} \\ $$$$\Rightarrow\frac{\mathrm{2x}}{\mathrm{2y}}=\frac{\mathrm{8}}{\mathrm{2}}\:\:\:\:\:\mathrm{or}\:\:\:\frac{\mathrm{2x}}{\mathrm{2y}}=\frac{−\mathrm{2}}{−\mathrm{8}} \\ $$$$\Rightarrow\frac{\mathrm{x}}{\mathrm{y}}=\mathrm{4}\:\:\:\mathrm{or}\:\:\frac{\mathrm{x}}{\mathrm{y}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by Rasheed.Sindhi last updated on 25/Aug/20
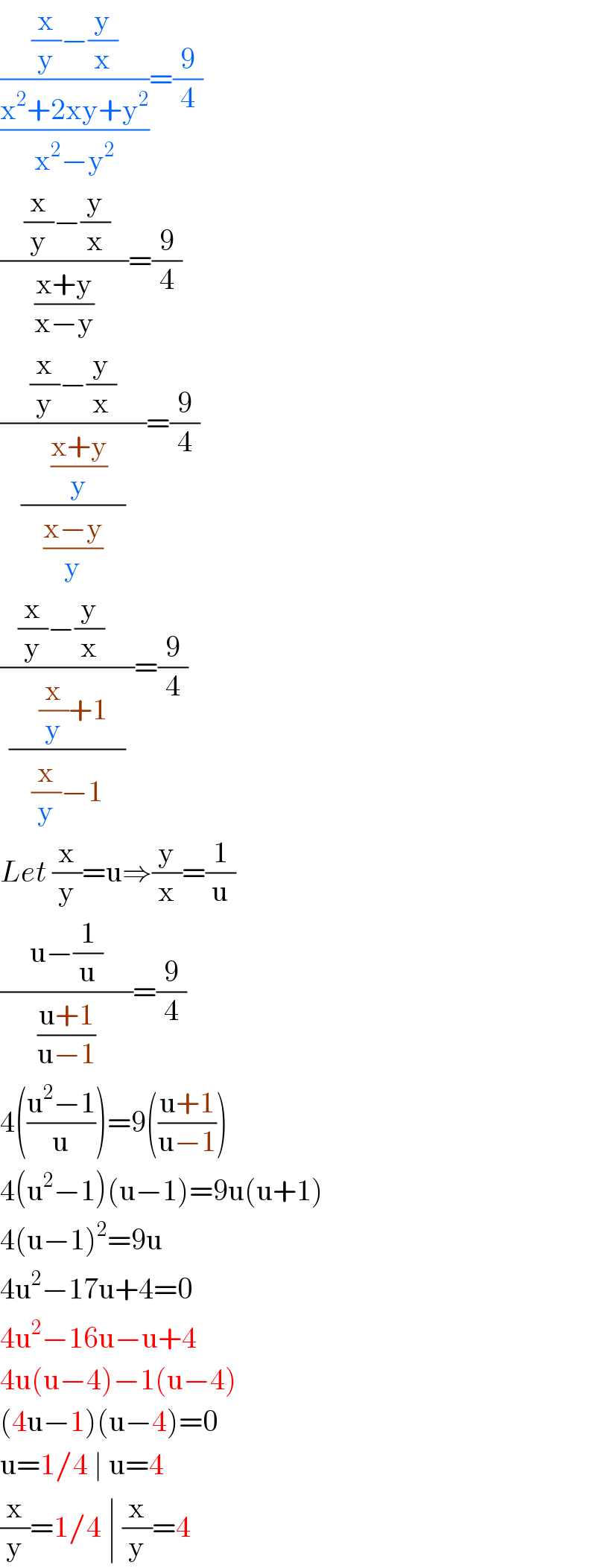
$$\frac{\frac{\mathrm{x}}{\mathrm{y}}−\frac{\mathrm{y}}{\mathrm{x}}}{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\frac{\:\:\:\:\frac{\mathrm{x}}{\mathrm{y}}−\frac{\mathrm{y}}{\mathrm{x}}\:\:\:}{\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\frac{\:\:\:\:\:\frac{\mathrm{x}}{\mathrm{y}}−\frac{\mathrm{y}}{\mathrm{x}}\:\:\:\:\:}{\frac{\:\:\:\:\:\frac{\mathrm{x}+\mathrm{y}}{\mathrm{y}}\:\:\:}{\frac{\mathrm{x}−\mathrm{y}}{\mathrm{y}}}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\frac{\:\:\:\frac{\mathrm{x}}{\mathrm{y}}−\frac{\mathrm{y}}{\mathrm{x}}\:\:\:\:\:}{\frac{\:\:\:\:\:\frac{\mathrm{x}}{\mathrm{y}}+\mathrm{1}\:\:\:}{\frac{\mathrm{x}}{\mathrm{y}}−\mathrm{1}}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$${Let}\:\frac{\mathrm{x}}{\mathrm{y}}=\mathrm{u}\Rightarrow\frac{\mathrm{y}}{\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{u}} \\ $$$$\frac{\:\:\:\:\:\mathrm{u}−\frac{\mathrm{1}}{\mathrm{u}}\:\:\:\:\:}{\frac{\mathrm{u}+\mathrm{1}}{\mathrm{u}−\mathrm{1}}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{4}\left(\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{u}}\right)=\mathrm{9}\left(\frac{\mathrm{u}+\mathrm{1}}{\mathrm{u}−\mathrm{1}}\right) \\ $$$$\mathrm{4}\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{u}−\mathrm{1}\right)=\mathrm{9u}\left(\mathrm{u}+\mathrm{1}\right) \\ $$$$\mathrm{4}\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{9u} \\ $$$$\mathrm{4u}^{\mathrm{2}} −\mathrm{17u}+\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{4u}^{\mathrm{2}} −\mathrm{16u}−\mathrm{u}+\mathrm{4} \\ $$$$\mathrm{4u}\left(\mathrm{u}−\mathrm{4}\right)−\mathrm{1}\left(\mathrm{u}−\mathrm{4}\right) \\ $$$$\left(\mathrm{4u}−\mathrm{1}\right)\left(\mathrm{u}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{u}=\mathrm{1}/\mathrm{4}\:\mid\:\mathrm{u}=\mathrm{4} \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}=\mathrm{1}/\mathrm{4}\:\mid\:\frac{\mathrm{x}}{\mathrm{y}}=\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by bobhans last updated on 25/Aug/20
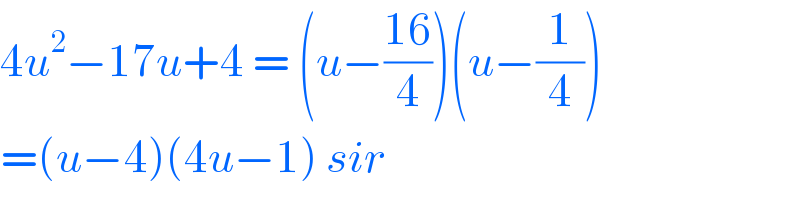
$$\mathrm{4}{u}^{\mathrm{2}} −\mathrm{17}{u}+\mathrm{4}\:=\:\left({u}−\frac{\mathrm{16}}{\mathrm{4}}\right)\left({u}−\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\left({u}−\mathrm{4}\right)\left(\mathrm{4}{u}−\mathrm{1}\right)\:{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 25/Aug/20
$$\mathcal{T}{hanks}\:{Bob}\:{for}\:{mentioning} \\ $$$${mistake}! \\ $$
Answered by Rasheed.Sindhi last updated on 25/Aug/20
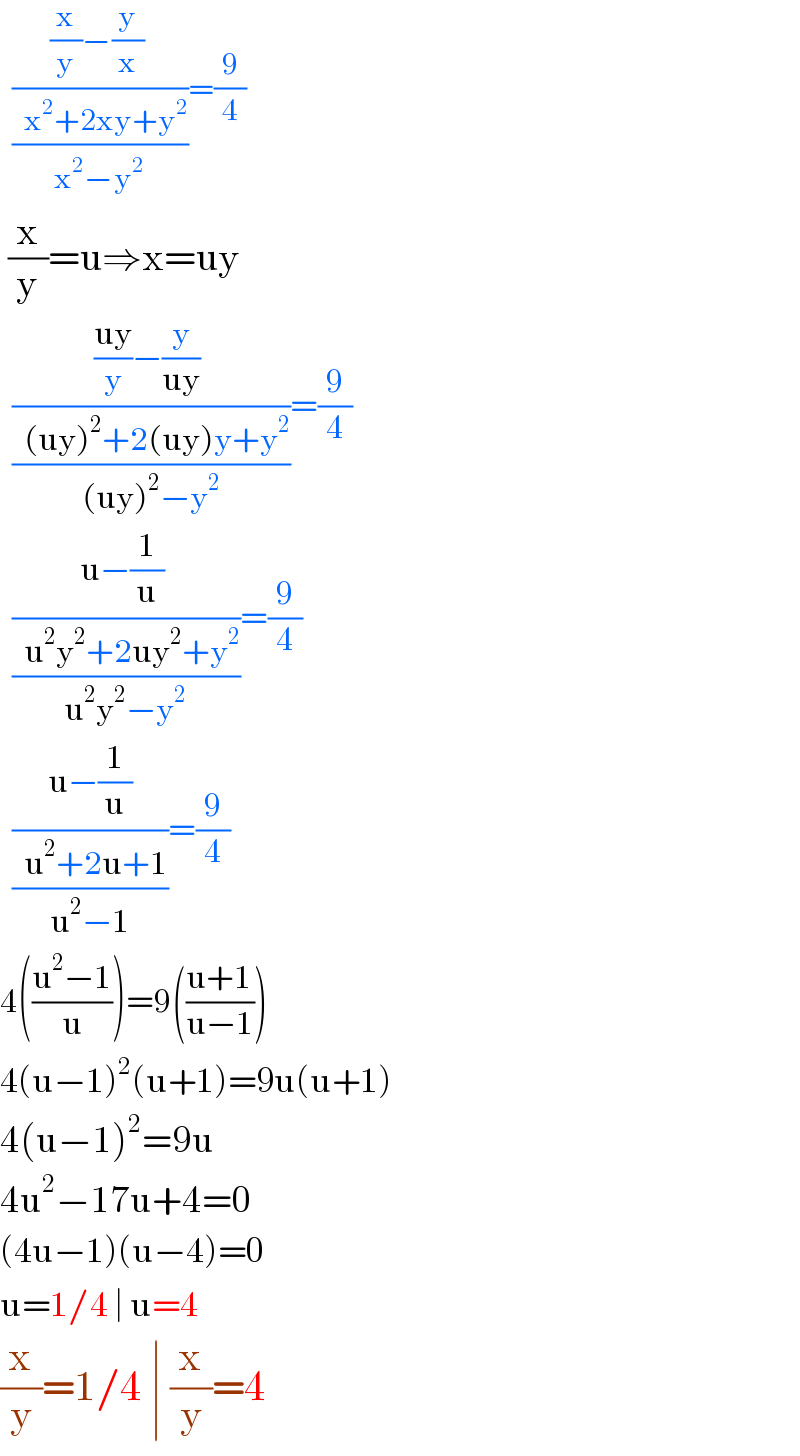
$$\:\:\frac{\:\frac{\mathrm{x}}{\mathrm{y}}−\frac{\mathrm{y}}{\mathrm{x}}\:\:}{\frac{\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\:\frac{\mathrm{x}}{\mathrm{y}}=\mathrm{u}\Rightarrow\mathrm{x}=\mathrm{uy} \\ $$$$\:\:\frac{\:\frac{\mathrm{uy}}{\mathrm{y}}−\frac{\mathrm{y}}{\mathrm{uy}}\:\:}{\frac{\:\:\left(\mathrm{uy}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{uy}\right)\mathrm{y}+\mathrm{y}^{\mathrm{2}} }{\left(\mathrm{uy}\right)^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\:\:\frac{\:\mathrm{u}−\frac{\mathrm{1}}{\mathrm{u}}\:\:}{\frac{\:\:\mathrm{u}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{2uy}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\:\:\frac{\:\:\:\mathrm{u}−\frac{\mathrm{1}}{\mathrm{u}}\:\:\:}{\frac{\:\:\mathrm{u}^{\mathrm{2}} +\mathrm{2u}+\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{4}\left(\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{u}}\right)=\mathrm{9}\left(\frac{\mathrm{u}+\mathrm{1}}{\mathrm{u}−\mathrm{1}}\right) \\ $$$$\mathrm{4}\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{u}+\mathrm{1}\right)=\mathrm{9u}\left(\mathrm{u}+\mathrm{1}\right) \\ $$$$\mathrm{4}\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{9u} \\ $$$$\mathrm{4u}^{\mathrm{2}} −\mathrm{17u}+\mathrm{4}=\mathrm{0} \\ $$$$\left(\mathrm{4u}−\mathrm{1}\right)\left(\mathrm{u}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{u}=\mathrm{1}/\mathrm{4}\:\mid\:\mathrm{u}=\mathrm{4} \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}=\mathrm{1}/\mathrm{4}\:\mid\:\frac{\mathrm{x}}{\mathrm{y}}=\mathrm{4} \\ $$
Answered by ajfour last updated on 25/Aug/20
![t=(x/y) (((t−(1/t)))/([(((t+1)^2 )/(t^2 −1))]))=(9/4) ⇒ 4(t^2 −1)^2 =9t(t+1)^2 t≠−1 ⇒ 4(t−1)^2 =9t 4t^2 −17t+4=0 t=((17)/8)±((√(289−64))/8) t = ((17±15)/8) = 4, (1/4) ⇒ t=(x/y) = (1/4), 4 .](https://www.tinkutara.com/question/Q109770.png)
$${t}=\frac{{x}}{{y}} \\ $$$$\frac{\left({t}−\frac{\mathrm{1}}{{t}}\right)}{\left[\frac{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{1}}\right]}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\Rightarrow\:\:\mathrm{4}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} =\mathrm{9}{t}\left({t}+\mathrm{1}\right)^{\mathrm{2}} \:\:\: \\ $$$$\:{t}\neq−\mathrm{1} \\ $$$$\Rightarrow\:\:\mathrm{4}\left({t}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{9}{t} \\ $$$$\mathrm{4}{t}^{\mathrm{2}} −\mathrm{17}{t}+\mathrm{4}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{17}}{\mathrm{8}}\pm\frac{\sqrt{\mathrm{289}−\mathrm{64}}}{\mathrm{8}} \\ $$$$\:{t}\:=\:\frac{\mathrm{17}\pm\mathrm{15}}{\mathrm{8}}\:=\:\mathrm{4},\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:\:\:{t}=\frac{{x}}{{y}}\:=\:\frac{\mathrm{1}}{\mathrm{4}},\:\mathrm{4}\:. \\ $$
Answered by 1549442205PVT last updated on 25/Aug/20
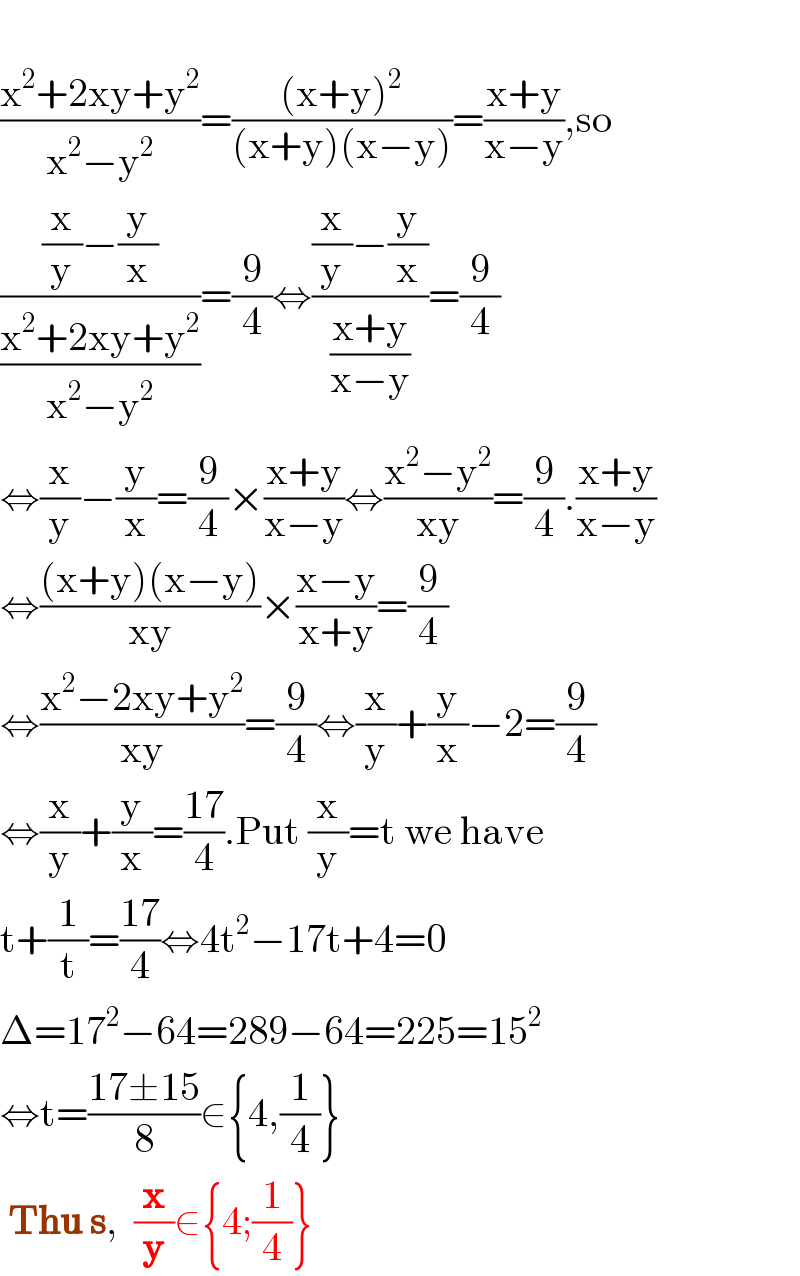
$$ \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }=\frac{\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} }{\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{x}−\mathrm{y}\right)}=\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}},\mathrm{so} \\ $$$$\frac{\frac{\mathrm{x}}{\mathrm{y}}−\frac{\mathrm{y}}{\mathrm{x}}}{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}=\frac{\mathrm{9}}{\mathrm{4}}\Leftrightarrow\frac{\frac{\mathrm{x}}{\mathrm{y}}−\frac{\mathrm{y}}{\mathrm{x}}}{\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\Leftrightarrow\frac{\mathrm{x}}{\mathrm{y}}−\frac{\mathrm{y}}{\mathrm{x}}=\frac{\mathrm{9}}{\mathrm{4}}×\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}\Leftrightarrow\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\mathrm{xy}}=\frac{\mathrm{9}}{\mathrm{4}}.\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}} \\ $$$$\Leftrightarrow\frac{\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{x}−\mathrm{y}\right)}{\mathrm{xy}}×\frac{\mathrm{x}−\mathrm{y}}{\mathrm{x}+\mathrm{y}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\Leftrightarrow\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} }{\mathrm{xy}}=\frac{\mathrm{9}}{\mathrm{4}}\Leftrightarrow\frac{\mathrm{x}}{\mathrm{y}}+\frac{\mathrm{y}}{\mathrm{x}}−\mathrm{2}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\Leftrightarrow\frac{\mathrm{x}}{\mathrm{y}}+\frac{\mathrm{y}}{\mathrm{x}}=\frac{\mathrm{17}}{\mathrm{4}}.\mathrm{Put}\:\frac{\mathrm{x}}{\mathrm{y}}=\mathrm{t}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}=\frac{\mathrm{17}}{\mathrm{4}}\Leftrightarrow\mathrm{4t}^{\mathrm{2}} −\mathrm{17t}+\mathrm{4}=\mathrm{0} \\ $$$$\Delta=\mathrm{17}^{\mathrm{2}} −\mathrm{64}=\mathrm{289}−\mathrm{64}=\mathrm{225}=\mathrm{15}^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{t}=\frac{\mathrm{17}\pm\mathrm{15}}{\mathrm{8}}\in\left\{\mathrm{4},\frac{\mathrm{1}}{\mathrm{4}}\right\} \\ $$$$\:\boldsymbol{\mathrm{Thu}}\:\boldsymbol{\mathrm{s}},\:\:\frac{\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{y}}}\in\left\{\mathrm{4};\frac{\mathrm{1}}{\mathrm{4}}\right\} \\ $$
