x-y-z-0-and-x-y-z-3-prove-that-x-5-1-12-y-5-1-12-z-5-1-12-xy-yz-zx-

Question Number 149474 by mathdanisur last updated on 05/Aug/21

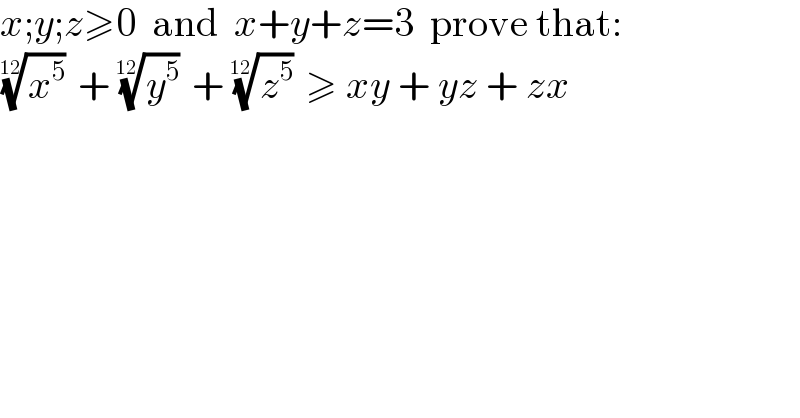
$${x};{y};{z}\geqslant\mathrm{0}\:\:\mathrm{and}\:\:{x}+{y}+{z}=\mathrm{3}\:\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\sqrt[{\mathrm{12}}]{{x}^{\mathrm{5}} }\:+\:\sqrt[{\mathrm{12}}]{{y}^{\mathrm{5}} }\:+\:\sqrt[{\mathrm{12}}]{{z}^{\mathrm{5}} }\:\geqslant\:{xy}\:+\:{yz}\:+\:{zx} \\ $$

Commented by dumitrel last updated on 06/Aug/21

$${hint}\:? \\ $$

Commented by mathdanisur last updated on 06/Aug/21

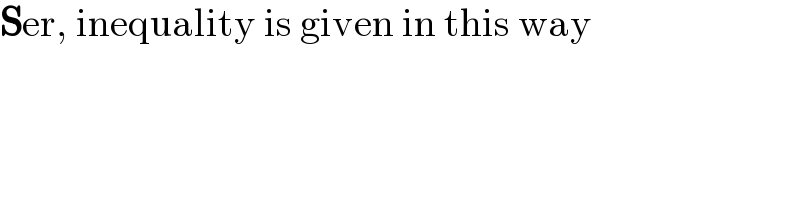
$$\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{given}\:\mathrm{in}\:\mathrm{this}\:\mathrm{way} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com